 |
|||
| HSG |
|
Aufgabenstellung
Robotik-Wettbewerb 2009 Das Labyrinth besteht aus festen, rechtwinkligen(!) Wänden und Elementen, die vom Roboter nicht verschoben werden können. Die Gesamtgröße beträgt maximal 4x4 Meter. Es gibt keine Räume sondern nur Gänge mit zahlreichen Abzweigungen und Kreuzungen, die Breite der Gänge (Rasterung) wird ungefähr zwischen 46cm und 54cm liegen (garantierte Mindestbreite für Dimensionierung des Roboters: 40cm). Der Boden besteht aus weißem bzw. hellem Papier, mit Ausnahme des dunkel markierten Feldes für das erste Szenario. Die Wände des Labyrinths sind ca. 20cm hoch.
Roboteraufbau
Bereits in einem frühen Stadium wurde beschlossen, den Roboter mit zwei Rädern und einer Abstützung bzw. 'Teerad' zu bauen. Mit Rädern ist er schneller als mit Raupen und er kann sich auch auf der Stelle drehen. Zur Erkundung der Umgebung sollte der Ultraschallsensor dienen, der mit dem dritten Motor wie ein Kopf drehbar angebracht werden sollte. Da die NXT-Motoren über Winkelsensoren verfügen, kann präzise nach vorne, links, hinten und rechts 'geschaut' werden. Wegen der Präzision sollte der US-Kopf direkt auf den Motor gesteckt werden. Der Motor muss also auf der Seite liegend eingebaut werden. Grundsätzlich besteht die Gefahr, dass der Roboter keine gerade Linie, sondern einen leichten Bogen fährt. Das hängt an der Unterschiedlichkeit der Motoren. Hier kann über die Winkelsensoren aber ein ungefährer Gleichlauf erreicht werden. Zur Schatzsuche braucht der Roboter einen Lichtsensor, der den Boden unter ihm beobachtet. Ein sehr großes Problem besteht darin, dass der Roboter sich vermutlich aufgrund unvermeidlicher Ungenauigkeiten aus der Mitte einer Rasterzelle entfernt. Wir gehen aufgrund der Angaben von Rasterzellen der Größe 50cmx50cm aus. Aufgrund dieses Maßes soll der Roboter seine aktuelle Rasterzelle bestimmen. Durch die Ultraschallmessung soll versucht werden, die 'Robotermitte' ca. 25cm vor einer Wand zu stoppen. Unser Roboter erhält zusätzlich eine druckempfindliche Stoßstange, die unabhängig vom restlichen Programm (eigener Thread) einen Kontakt erkennen kann. Da der Roboter aufgrund aufgelaufener Ungenauigkeiten eine Wand auch schräg anfahren kann, soll nach einem Kontakt nach kurz weitergefahren werden. Der Roboter soll sich dadurch an der Wand ausrichten. Anschließend soll er seine Mitte wieder 25cm entfernen. Erste Konstruktionen wurden verworfen, weil der relativ schwere Brick zu weit oben angeordnet zu einem hohen Schwerpunkt führt. Dadurch kann der Roboter bei schnellen Drehungen umkippen. Die gewählte Lösung entspricht etwa dem 'Explorer' plus zusätzlichem Lichtsensor. Auf diese Weise ist auch der Bau dokumentiert und leicht zu reproduzieren.
Roboterprogrammierung
Über die Links
- 7 Tiefensuche - Taschenbuch der Algorithmen
- 8 Der Pledge-Algorithmus - Taschenbuch der Algorithmen
- 9 Zyklensuche in Graphen - Taschenbuch der Algorithmen
- Backtracking - wikipedia
- Backtracking - www.matheprisma.uni-wuppertal.de
- Iterative Tiefensuche - wikipedia
- Von Ameisen, Bibern, Käfer, Mäusen und Labyrinthen - Horst Müller, Universität Erlangen-Nürnberg
informierten wir uns über in Frage kommende Algorithmen. Um die Algorithmen zu studieren, beschlossen wir grafische Simulationen zu schreiben, so kann man in dem Python31-Programm laby31.py unseren Algorithmus in Aktion bewundern.
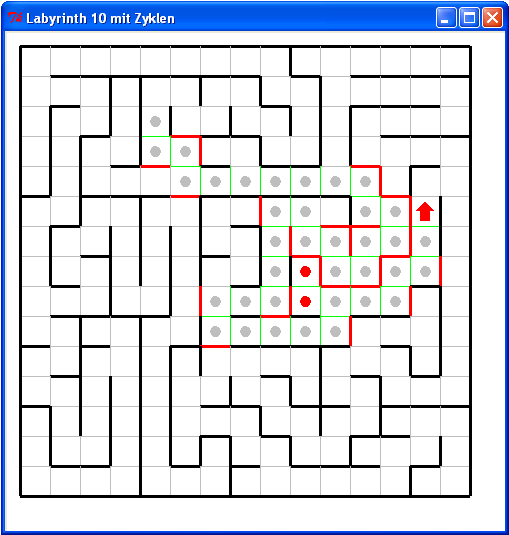
Dabei bedeuten schwarze Linien Wände in der 'Welt', graue Linien sind Zellengrenzen in der 'Welt'. Die 'graue und schwarze Welt' kennt der Roboter nicht. Eine rote Linie bedeutet eine vom Roboter erkannte Wand, eine grüne Linie eine vom Roboter erkannte überschreitbare Zellengrenze, graue Punkte markieren den bisherigen vom Roboter gespeicherten Weg, rote Punkte markieren vom Roboter erkannte 'Sackgassenzellen'.
Schon in einem frühen Stadium war uns klar, dass wir im Hinblick auf das später auf dem NXT laufende Programm beim Roboterverhalten auf eine einfache Daten- und Kontrollstrukturen achten mussten. Unser Roboter speichert sein Wissen über die 'Welt' in einem zweidimensionalen Array. Dieses Array enthält auch Informationen über den begangenen Weg und über erkannte Sackgassen. Da die von uns gewählte Sprache NXC über keine Rekursion verfügt, haben wir auch bereits in der Simulation einen Stack eingeführt. Der Stack enthält den bereitsgegangenen Weg plus eine Information über die letzte Drehung bevor die aktuelle Zelle betreten wurde. Auf diese Weise ist gegebenenfalls ein 'Backtracking' möglich. Beim Rückwärtsgehen wird dann die verlassene Zelle als 'Sackgasse' markiert. Sackgassen werden später nicht mehr betreten. Natürlich werden Sackgassenzellen vom Stack genommen.
Das 'Gedächtnis' z
Der Roboter speichert seine Erkenntnisse in einem zweidimensionalen Array z. Das Array ist nach Zeilen und Spalten organisiert und enthält Bytes. Wir haben eine eindeutige Zuordnung der Wände zu einer Zelle dadurch erreicht, dass jede Zelle nur Information über oben bzw. vorne und links speichert. Die rechte Wand einer Zelle wird also als linke Wand der rechten Nachbarzelle verwaltet. Für die untere bzw. hintere Wand gilt entsprechendes. Über jede Zellgrenze ist zu speichern, ob der Roboter weiß, dass sich dort keine Wand oder eine Wand befindet oder dass er über diese Zellgrenze noch nichts weiß. Zu Beginn weiß der Roboter nichts außer der aktuellen Zeile und Spalte. Um negative Zahlen bei den Indizes zu vermeiden starten wir mit Zeile 20 und Spalte 20. Auf diese Weise passt die erkundete Welt sicher in das Array. Die Information zu einer Zelle wird nun folgendermaßen codiert: Bit 1 ist das 'Wissensbit' für oben. Ist es gesetzt, so bedeutet das, dass der Roboter über die obere Zellgrenze Bescheid weiß. Bit 0 = 1 bedeutet dann Wand, Bit 0 = 0 bedeutet keine Wand. Entsprechend werden die Informationen über die linke Zellgrenze in Bit 3 und Bit 2 gespeichert: 00 und 01: weiß nicht, 10: keine Wand, 11: Wand. Das nächste Bit 4 verwenden wir, um eine Zelle als zum Weg gehörend zu kennzeichen. Bit 5 ist das 'Sackgassen-Bit'.
Die Bewegung des Roboters
Idealtypisch macht der Roboter nur die Bewegungen fd(): um Rastermaß vorwärts, bk(): um Rastermaß rückwärts, lt(): Linksdrehung um 90°, rt(): Rechtsdrehung um 90°. Der Roboter speichert seine aktuelle Orientierung in einer Variablen orientierung. Wir haben dabei codiert: 0 = vorne/oben, 1 = links, 2 = hinten/unten und 3 = rechts. Mit der Orientierungsinformation wird die aktuelle Position bei einer Bewegung entsprechend angepasst. Beim Start schaut unser Roboter definitionsgemäß nach vorne.
Die Erkundung der Umwelt
Über seinen 'US-Kopf' kann der Roboter nach vorne, links, hinten und rechts 'schauen' und aus der Messung entscheiden, ob die jeweilige Zellgrenze frei ist. Eine Funktion frei(richtung) ermittelt entweder aus dem Gedächtnis oder durch Messung, ob eine Zelle betretbar ist. Eine Nachbar-Zelle ist nicht (direkt) betretbar, wenn eine Wand im Weg ist oder wenn die Zelle bereits als Sackgasse oder Weg markiert ist. Auf diese Weise werden also aussichtslose Wege oder Schleifen vermieden. Natürlich wird das Ergebnis einer Messung in das 'Gedächtnis' eingetragen.
Die Schatzsuche
Der Roboter beobachtet laufend über den Lichtsensor den Boden. Ist der Boden dunkel, so wird die aktuelle Position als Schatzposition gespeichert und über das Display ausgegeben.
Algorithmus als Pseudo-Code
def sucheZiel():
# Startzelle auf Stack
stack.push((rz,rs,vorne)) # (Zeile, Spalte, Richtung)
# als Weg markieren
z[rz,rs] = SetBit(4,z[rz,rs])
# Suchschleife
while not amZiel():
# top of stack lesen
(rz,rs,richtung) = stack.pop()
stack.push((rz,rs,richtung))
# Umgebung untersuchen
# vorne
if not amZiel() and frei(vorne) : # frei(vorne) untersucht Welt nach vorne
# und macht Eintragungen im 'Gedächtnisarray'
fd() # um Rastermaß vorwärts, Koordinaten werden akualisiert
stack.push((rz,rs,vorne))
# als Weg markieren
z[rz,rs] = SetBit(4,z[rz,rs])
# links
elif not amZiel() and frei(links):
lt() # linksdrehen um 90°
fd()
stack.push((rz,rs,links))
# als Weg markieren
z[rz,rs] = SetBit(4,z[rz,rs])
# Ausgangszelle auch nach hinten untersuchen
elif (len(self.stack) == 1) and not ziel and frei(hinten):
lt()
lt()
fd()
stack.push((rz,rs,hinten))
# als Weg markieren
z[rz,rs] = SetBit(4,z[rz,rs])
# rechts
elif not amZiel() and frei(rechts):
rt() # rechts drehen um 90°
fd()
stack.push((rz,rs,rechts))
# als Weg markieren
z[rz,rs] = SetBit(4,z[rz,rs])
else:
# keinen Ausweg gefunden
# Zelle als Sackgasse markieren
z[rz,rs] = SetBit(5,z[rz,rs])
# pop
(zeile,spalte,orientierung) = stack.pop()
# rückwärts gehen
if orientierung == vorne:
bk() # um Rastermaß rückwärts
elif orientierung == links:
bk()
rt()
elif orientierung == hinten:
bk()
lt()
lt()
elif orientierung == rechts:
bk()
lt()
Die Wahl der Programmiersprache
Die Sprache NXC wurde gewählt, weil sie als weit leistungsfähiger als Lego-Next-G beschrieben wird. Die Sprache ist multithread-fähig und verspricht durch ihre Nähe zu C eine - verhältnismäßig - leichte Erlernbarkeit. Dass z.B. eine PID-Regelung der Motoren verfügbar ist, erhöhte unser Vertrauen in die 'Professionalität' der Sprache. Trotz allem ist in der Kürze der Zeit keine umfassend begründete Entscheidung zu fällen. Es ist eine große Herausforderung, in kurzer Zeit eine neue Sprache mit neuen Konzepten z.B. Threads zu lernen. Die Verwendung mehrdimensionaler Arrays machte ein Patchen der Lego-Firmware notwendig.
Zur Erzeugung und Abspeicherung von Labyrinthen dient das Python31-Programm LabyGen2.py. Bit 0 codiert oben, Bit 1 codiert links. Zur Darstellung der rechten und unteren Grenze ist also eine Zusatzspalte bzw. Zusatzzeile erforderlich. Labyrinthe mit Schleifen wurden durch von Hand duchgeführte Veränderungen erzeugt.
Probleme bei der Simulation
In der Simulation ist die 'Welt' nicht einfach da, sondern muss eigens abgespeichert werden. Da der Roboter irgendwo in irgendeiner Orientierung in die 'Welt' gesetzt wird, ergibt sich die Schwierigkeit, zwischen 'Welt-System' und 'Roboter-System' zu transformieren. Trotz allen Aufwandes ermöglicht die Simulation ein Studium unserer Algorithmen und eine Demonstration möglicher Fehler.
Die Umsetzung in NXC
Leider fehlte gegen Schluss der Vorbereitung die nötige Zeit, NXC genügend sicher zu beherrschen. So wurde der Algorithmus anscheinend nicht korrekt im Roboter umgesetzt. Schade! Die Programme findet man an anderer Stelle.
Nicht bewältigter Testfall
Im Labyrinth test0.txt ging der in Zeile 0, Spalte 2 mit Orientierung 0 gestartete Roboter (fin_v3) in Zeile 1, Spalte 1 fälschlich rückwärts. In der Simulation gab es dagegen keine Probleme.
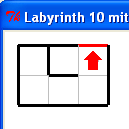
Das Debuggen am Roboter ist so mühsam, dass wir alle interessierenden Daten per Bluetooth an einen PC übertragen sollten!
Zwischenstand
laby7.py, laby1.txt, (ohne Rekursion, mit Stack) laby8.py, laby2zyklus.txt, laby9.py, laby10.py, LabyGen2.py, test2.txt
Links
- Robotik-Wettbewerb 2009
- 7 Tiefensuche - Taschenbuch der Algorithmen
- 8 Der Pledge-Algorithmus - Taschenbuch der Algorithmen
- 9 Zyklensuche in Graphen - Taschenbuch der Algorithmen
- Backtracking - wikipedia
- Backtracking - www.matheprisma.uni-wuppertal.de
- Backtracking mit Heuristiken - www.swisseduc.ch
- Backtracking - www.zotteljedi.de
- LEGO/ProjektSS08 - www.wi.hs-wismar.de
- lego_basis_workshop.pdf - xserve2-1.et.fh-osnabrueck.de
- Projekte2007/T2-Garrison - www.wi.hs-wismar.de
- Maus im Labyrinth - Oliver Meincke
- Graphenalgorithmen - Visage
- Netzwerk-AG:Robotik - lehrer.gym-oppenheim.de/Kutschinski
- Iterative Tiefensuche - wikipedia
- www.nxtasy.org
- Von Ameisen, Bibern, Käfer, Mäusen und Labyrinthen - Horst Müller, Universität Erlangen-Nürnberg
- NXC_MotorControl
- NXC - www.debacher.de
- NXC-Hilfe.pdf
- NXC - wikipedia
- NXC-Tutorial.pdf - deutsch
![]()