Darstellung ganzer Zahlen

• Darstellen von Integer - wikipedia
• Zweierkomplement - wikipedia
• Bytereihenfolge - wikipedia
• BytesToInt.zip

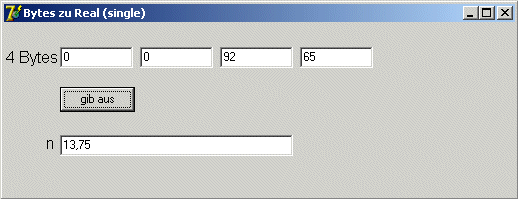
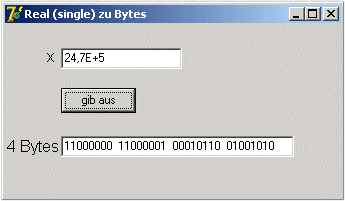
Darstellung einer 4-Byte-Real-Zahl (single) nach IEEE 754

Als Beispiel soll die Zahl +13,75 dargestellt werden.

1. Zuächst wird die Zahl |x| binär dargestellt: |x| = 13,75₁₀ = 1101,11₂
   Im Binärsystem (siehe auch: Stellenwertsystem) haben die Nachkommastellen die Wertigkeit 1/2, 1/4, 1/8, 1/16, ... .
   0,1₁₀ wird dann zu 0,00011₂, also periodisch. (binaerbruch.zip)
2. Jetzt wird das Komma so verschoben, dass für die Mantisse m' 1<=m'<2 gilt: |x| = 1,10111*2³.
   Es gilt also jetzt Mantisse m' = 1,10111 und Exponent e' = 3₁₀
3. Bei dieser normalisierten Darstellung ist das Bit vor dem Komma immer gesetzt. Man muss es nicht speichern (hidden bit), aber man darf nicht vergessen, dass es da ist. Im single-Format für Delphi bzw float für C ist die Mantisse 23 Bit groß. Da wir nur die Nachkommastellen speichern, füllen wir mit Nullen auf:
   m = 101110 00000000 00000000
4. Im Format single/float wird der Exponent mit 8 Bit dargestellt, dabei werden negative Zahlen nicht im Zweierkomplement, sondern mit einem Versatz, genannt Bias , gespeichert. Der Versatz beträgt beim Format single/float 127. Haben wir also einen Exponenten 3, so müssen wir 3+127= 130 abspeichern. Zur Interpretation muss man also von der gespeicherten Zahl 127 abziehen.
   Es gilt also e = 130₁₀ = 128₁₀+2₁₀ = 1000 0010₂
5. Das Vorzeichen s (sign) wird mit 0 gespeichert, da x positiv ist.
6. Insgesamt ergibt sich:
   
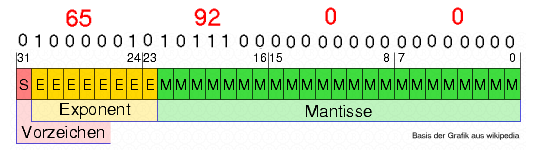
7. Da die Bytes auf einem Windowsrechner little-endian (niederwertigstes Byte zuerst) abgespeichert werden, sollte die Zahl als 0 0 92 65 gespeichert werden.

Überprüfung mit Python 'struct'

Es wird -13,75 in die 4-Byte-C-Struktur 'float' umgewandelt. Der Bequemlichkeit halber wird big-endian dargestellt.

>>> from struct import *
>>> from StrToHexBin import *
>>> pack('>f',-13.75)
'\xc1\\\x00\x00'
>>> s2b(pack('>f',-13.75))
'  1100 0001  0101 1100  0000 0000  0000 0000'

Wir lesen ab: Vorzeichen : 1, Exponent: 1000 0010, Mantisse (ohne hidden bit): 101 1100 0000 0000 0000 0000

Wieso funktioniert hier eigentlich ...

Aufgabe

Wandle 0.1 in das 4-Byte-float-Format um. Erläutere, warum

a = 1
while a != 0:
    a = a - 0.1

in Python nicht terminiert. Wie stellt Python 'float' dar? Was ist die größte, was die kleinste float-Zahl auf deinem System?

>>> s2b(pack('>f',0.1))
'  0011 1101  1100 1100  1100 1100  1100 1101'
>>> pack('>f',0.1)
'=\xcc\xcc\xcd'
>>> unpack('>f','=\xcc\xcc\xcd')
(0.10000000149011612,)

Überprüfung mit einem Delphi-Programm

BytesToReal.zip

Um die Bytes einer real-Zahl direkt zu manipulieren, kann man einerseits mit absolute den Speicherplatz der real-Variablen an die gleiche Stelle wie den eines Byte-Arrays legen oder eine Typ-Umwandlung vornehmen. Im folgenden Quelltext-Ausschnitt sind beide Methoden angewandt, eine könnte also weggelassen werden. Ausprobieren!

procedure TForm1.bGibausClick(Sender: TObject);
type
  Tbyte4 = array[1..4] of byte;
var
  b : Tbyte4;
  x : single absolute b; // x wird an die gleiche Adresse wie b gelegt
begin
  b[1] := StrToInt(eB1.Text); b[2] := StrToInt(eB2.Text);
  b[3] := StrToInt(eB3.Text); b[4] := StrToInt(eB4.Text);

  x := single(b); // Byte-Array wird zu single umgewandelt

  eX.Text := FloatToStr(x);
end;

Analyse der Darstellung von real-Zahlen

RealToBytes.zip