 |
|||
| HSG |
|
Aufgabe
Es soll ein einfacher Funktionsplotter geschrieben werden.
Transformation Welt --> Bild
Ein Grundproblem der Grafik-Programmierung ist die Transformation sogenannter Welt-Koordinaten (x/y) auf Bildschirm-Koordinaten (u/v). Im Folgenden soll anhand eines Beispiels die Entwicklung der Transformation gezeigt werden:
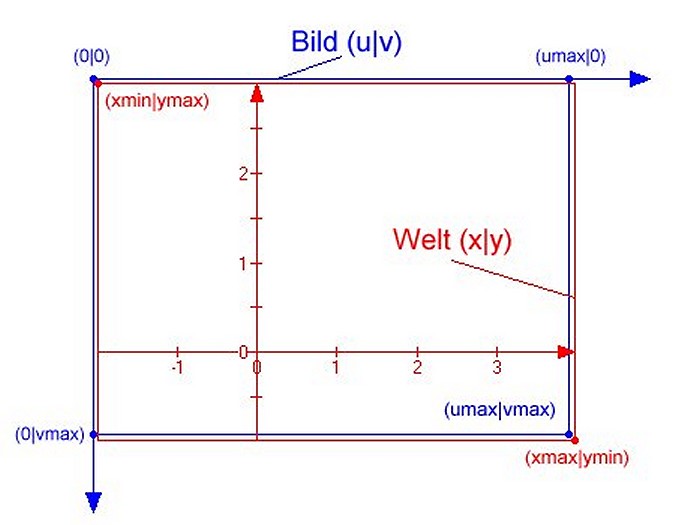
Ansatz
u = a*x + b und v = c*y + d
gesucht: Koeffizienten a, b, c, d
Gleichungen
|
|
Lösungen
III - I:
umax - 0 = a(xmax - xmin) => a = umax/(xmax-xmin)
a in I:
b = - a*xmin
IV - II:
vmax - 0 = c(ymin - ymax) => c = vmax/(ymin-ymax)
c in II:
d = - c*ymax
Teilaufgabe 1
- Lege ein Delphi-Projekt 'Plotter0' an, das eine Image-Komponente 'iBild' enthält. 'iBild' soll 640 Pixel breit und 480 Pixel hoch sein.
- Vereinbare die Attribute (Variablen, die zum Objekt gehören) a,b,c,d vom Typ 'real' .
- Vereinbare die Methoden (Prozeduren und Funktionen, die zum Objekt gehören)
berechne_Koeffizienten, ut und vt.
Das sieht dann so aus:
... private a,b,c,d,xmin,xmax,ymin,ymax : real; procedure berechne_Koeffizienten(pxmin,pxmax,pymin,pymax : real; umax,vmax : integer); function ut(x : real) : integer; function vt(y : real) : integer; public { Public-Deklarationen } ... - Implementiere im Implementation-Teil die Prozeduren und Funktionen aus dem Interface-Teil.
Dabei werden die Prozedur- und Funktionsköpfe (Signaturen) wiederholt und die zugehörigen Anweisungen angegeben.
Um die Methoden der richtigen Klasse zuzuordnen, muss vor dem Namen der Methode der
Name der Klasse durch einen Punkt getrennt stehen.
Das sieht dann so aus:
... procedure TForm1.berechne_Koeffizienten(pxmin,pxmax,pymin,pymax : real; umax,vmax : integer); begin // Grenzen in Attributen 'merken', 'p' steht für 'Parameter' xmin := pxmin; xmax := pxmax; ymin := pymin; ymax := pymax; // Koeffizienten berechnen a := umax/(xmax-xmin); b := -a*xmin; c := vmax/(ymin-ymax); d := -c*ymax; end; function TForm1.ut(x : real) : integer; begin result := Round(a*x+b); end; function TForm1.vt(y : real) : integer; begin result := Round(c*y+d); end; ...
- Bevor man etwas zeichnet, müssen die Koeffizienten a,b,c,d berechnet sein. Das könnte man durch einen Button-Klick
erledigen. Eleganter geht es, wenn man die Berechnung an das Ereignis OnCreate des Formulars bindet. Dazu
muss man im Objekt-Inspektor die Seite Ereignisse anwählen und die Ereignisbehandlung zu OnCreate durch einen
Doppelklick im entsprechenden Feld im Editor aufrufen.
Das sieht dann so aus:
... procedure TForm1.FormCreate(Sender: TObject); begin berechne_Koeffizienten(-2,4,-1,3,639,479); // iBild.width wurde auf 640, iBild.height auf 480 eingestellt end; ...
- Jetzt soll die x-Achse gezeichnet werden. Die x-Achse in unserer Welt verläuft von
(-2/0) nach (4/0). Diese
Welt-Koordinaten sollen jetzt in Bild-Koordinaten transformiert werden. Zu diesem Zweck dienen die
Funktionen ut und vt. Die notwendige Typ-Umwandlung zu integer erledigen sie übrigens 'nebenbei'.
Die Ereignisbehandlungsroutine könnte etwa so aussehen:
procedure TForm1.bZeichneAchsenClick(Sender: TObject); begin iBild.canvas.MoveTo(ut(-2),vt(0)); iBild.canvas.LineTo(ut(4),vt(0)); // .... end;
- Das funktioniert, ist aber wenig elegant und kostet viel Schreibarbeit. Eine typische Situation, wo eine Prozedur
Linie angebracht wäre. Wo muss der Interface-Teil, wo der Implementation-Teil untergebracht werden? Wie kann das
Zeichnen der Achsen vereinfacht werden?
procedure TForm1.Linie(x1,y1,x2,y2 : real); // zeichnet eine Linie von (x1/y1) nach (x2/y2) begin iBild.canvas.MoveTo(ut(x1),vt(y1)); iBild.canvas.LineTo(ut(x2),vt(y2)); end;
Teilaufgabe 2
- Zeichne die kleinen Skalierungsstriche auf die Achsen (for-Schleifen!).
- Verwende die canvas-Methode TextOut in Verbindung mit ut und vt, um die Achsen zu beschriften.


- Zeichne die Pfeile an die Achsen.
Teilaufgabe 3
- Vereinbare eine Funktion f(x : real) : real).
- Zeichne den Graphen zu f.
- Zeichne nur einen Abschnitt des Graphen.
