 |
|||
| HSG |
|
Formale Verifikation am Beispiel der ägyptischen Bauern-Multiplikation
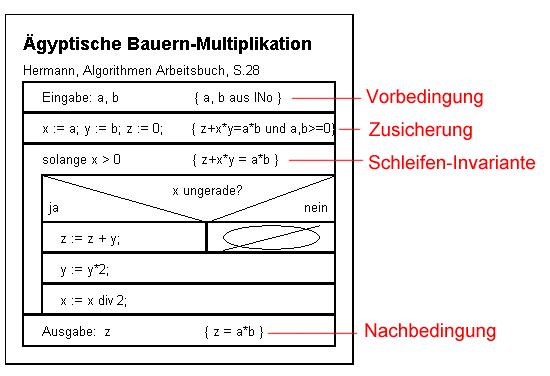
Es ist aus der Gültigkeit der Vorbedingung die Gültigkeit der Nachbedingung zu zeigen. Aus der Zusicherung {z + x*y = a*b und a,b >= 0} folgt die Gültigkeit der Schleifeninvariante { z + x*y = a*b } zu Beginn der Schleife.
Wir zeigen, dass die Schleifeninvariante nach Durchlaufen des Schleifenkörpers invariant bleibt. Die Werte der Variablen x,y,z nach Durchlaufen des Schleifenkörpers nennen wir x',y',z'.
Es gibt zwei Fälle:
- x ist ungerade
z' = z+y; y' = 2*y; 2*x'+1=x bzw. x' = (x-1)/2;
=>
z' + x'*y' = z+y + (x-1)/2 * 2*y = z+y + (x-1)*y = z+y + x*y - y = z + x*y .
- x ist gerade
z' = z; y' = 2*y; x' = x/2;
=>
z' + x'*y' = z + x/2 * 2*y = z + x*y.
Die while-Schleife terminiert sicher (kommt zu einem Ende), da x ganzzahlig halbiert wird.
Damit ist formal bewiesen, dass der Algorithmus tatsächlich das Produkt liefert.
Bemerkung:
Der Algorithmus hat eine große Bedeutung für das binäre Multiplizieren, denn im Binär-System ist das Multiplizieren mit 2 und das Dividieren durch 2 so einfach wie das Multiplizieren mit 10 und das Dividieren durch 10 im Zehner-System. Ebenso muss man sich, um festzustellen, ob eine Zahl ungerade ist, nur ein Bit ansehen.
Aufgabe:
Der Programm-Abschnitt
x := a; y := b; p := 0; while x > 0 do begin p := p+y; x := x-1; end;
beschreibt einen Algorithmus.
Überlege, was die Ein- und Ausgaben sein könnten und was der Algorithmus tut.
Beschreibe den Algorithmus informell in einem Satz.
Beweise formal durch Zusicherung deine Angaben.
Zeichne ein Struktogramm einschließlich der Zusicherungen.