 |
|||
| HSG |
|
Frequently we need to traverse a Prolog structure and calculate a result that depend on what was found in the structure. At intermediate stages of the traversal, we will have an interim value for the result. A common technique is to use an argument of the predicate to represent "the answer so far". The argument is called an accumulator.
Clocksin/Mellish, Programming in Prolog, S.67
Beispiel
nach Clocksin/Mellish, Programming in Prolog, S.68listlen(L,N):-listlen(L,0,N). listlen([],A,A). listlen([K|R],A,N):-A1 is A+1,listlen(R,A1,N).Es wird ein Hilfsprädikat listlen(L,0,N) benutzt, das - wie hier - häufig den gleichen Funktor wie das ursprüngliche Prädikat hat, sich aber durch die Stelligkeit unterscheidet. Es kommt der Akkumulator dazu, der hier anfänglich mit 0 gefüllt wird (es hat sich noch nichts angesammelt).
Die Rekursion bricht ab, wenn die leere Liste erreicht ist. Jetzt wird der Akkuinhalt in die Lösungsvariable übertragen.
Der Rekursionsschritt besteht darin, den Kopf der Liste abzutrennen und für den Rest der Liste das Prädikat mit um 1 erhöhten Akkumulator wieder aufzurufen.
Die Lösungsvariable - hier N - bleibt über die Rekursion immer gleich. So transportiert sich die Lösung von der Rekursionsbasis zum aufrufenden Prädikat.
Veranschaulichung im Schachteldiagramm
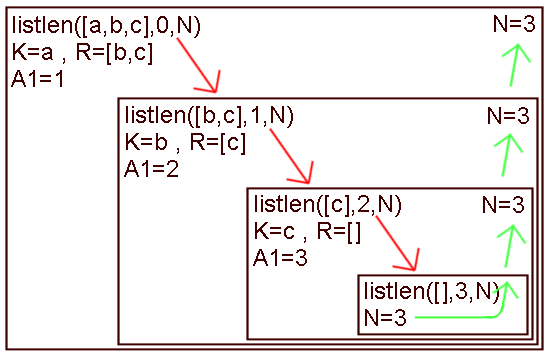
Im Akkumulator kann natürlich auch eine sich erweiternde Liste - wie bei der Tiefensuche - gespeichert werden.