 |
|||
| HSG |
|
Breitensuche verfolgt von Anfang an alle möglichen Wege. Man findet also automatisch einen minimalen Weg zuerst.
Prolog-Programm (nach Informatik mit Prolog, Gerhard Röhner, S.63)
kante(a,b).
kante(a,c).
kante(b,d).
kante(b,e).
kante(c,e).
kante(c,f).
kante(d,g).
kante(e,f).
kante(e,g).
kante(e,h).
kante(f,i).
kante(g,h).
kante(g,j).
kante(h,i).
kante(h,k).
kante(i,m).
kante(j,k).
kante(k,m).
verbunden(A,B):- kante(A,B).
verbunden(A,B):- kante(B,A).
breitensuche(Start,Ziel,Loesung):-breitensuche([Start],[],Ziel,Loesung).
breitensuche(Pfad,Pfade,Ziel,Loesung):-Pfad=[Ziel|_],Pfad=Loesung,!.
breitensuche(Pfad,Pfade,Ziel,Loesung):-Pfad=[KnotenA|_],
findall([KnotenN|Pfad],
(verbunden(KnotenA,KnotenN),not(member(KnotenN,Pfad))),
GefundenePfade),
append(Pfade,GefundenePfade,NeuePfade),
NeuePfade=[PfadN|RestPfade],
breitensuche(PfadN,RestPfade,Ziel,Loesung).
Erläuterungen zu breitensuche(Pfad,Pfade,Ziel,Loesung):
- Zunächst wird überprüft, ob der Kopf (der Pfad wird umgedreht aufgebaut) des aktuellen Pfades der Zielknoten ist. Ist das der Fall, so wird der Pfad als Lösung ausgegeben und mit einem Cut die Suche nach weiteren Lösungen abgebrochen.
- Im Rekursionsfall wird zunächst der aktuelle KnotenA dem aktuellen Pfad entnommen.
- Mit findall werden alle Verbindungen zu neuen KnotenN gesucht, die nicht im bisherigen Pfad (Zyklen vermeiden!) enthalten sind. In die Lösungsliste werden aber jeweils komplette Pfade (bisheriger Pfad ergänzt um den KnotenN) eingetragen.
- Die eben gefundenen Pfade werden an die Liste der übergebenen Pfade angehängt.
- Die gerade entstandene Liste der Pfade wird in den Kopf PfadN und den Rest RestPfade aufgetrennt.
- breitensuche wird rekursiv aufgerufen mit PfadN als aktuellem Pfad und RestPfade als Pfadliste. Es wird also gewissermaßen der Kopf der Liste Pfade abgetrennt und bearbeitet.
Arbeitsweise des Algorithmus am Beispiel breitensuche(e,i,L)
Es soll ein Weg von e nach i gesucht werden. In einem ersten Schritt werden alle Weg, die von e ausgehen,
aufgelistet. Sie alle könnten als Anfang des gesuchten Lösungswegs dienen. Die Reihenfolge, in der die Wege
aufgelistet werden, ergibt sich aus der Wissensrepräsentation. In obiger Prolog-Implementierung ist ein Weg
rückwärts zu lesen, dh. [d,f,e] steht für den Weg von e über f nach d. Das zweite Argument von
breitensuche/4 ist eine Liste, die die Teilwege als Listen speichert.
Der Lösungsweg muss einen der aufgelisteten Teilwege als Anfang haben. Mangels besserer Information werden
nun alle Teilwege der Reihe nach bearbeitet. Diese Bearbeitung besteht zunächst darin, dass geprüft wird,
ob das Ziel schon erreicht ist. Wenn ja, endet der Algorithmus. Wenn nein, wird der Teilweg auf alle möglichen
Arten erweitert. Die erweiterten Teilwege werden hinten an die Liste der zu bearbeitenden Teilwege angehängt.
Der aktuell bearbeitete Weg wird gestrichen. Da jeweils der erste Teilweg der Liste bearbeitet wird, kann es
sein, dass eine bereits gefundene Lösung erst entdeckt wird, wenn die Lösung ganz nach oben gerückt ist.
Der Weg e-g kann auf drei Arten zu e-g-h, e-g-j und e-g-d erweitert werden.
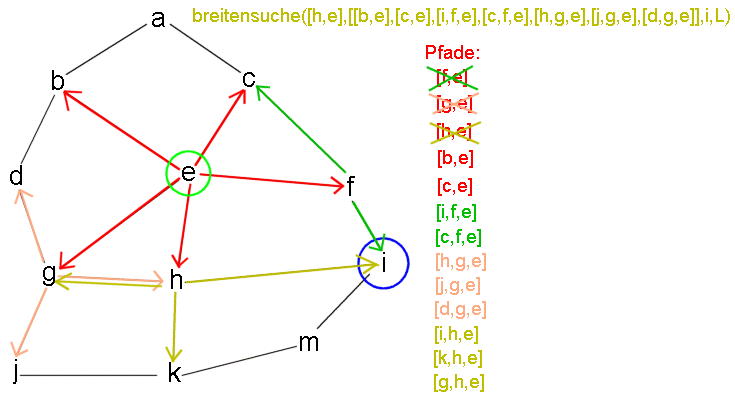
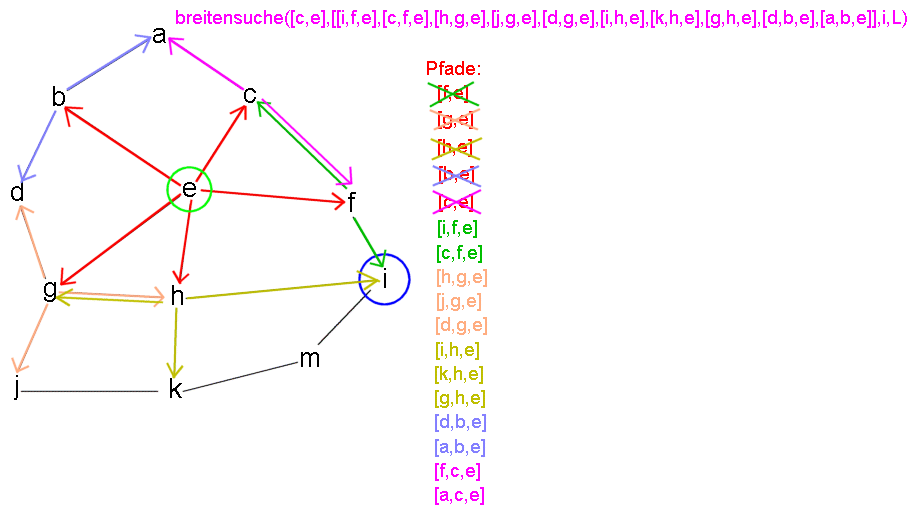
Der Kopf der aktuellen Liste ist das Ziel, der Algorithmus bricht ab.
