 |
|||
| HSG |
|
Beim Resolutionsverfahren wird das Gegenteil der zu beweisenden Formel angenommen und versucht, die Annahme zum Widerspruch zu führen. Damit das Verfahren maschinell durchführbar wird, muss vorher die Ausgangsformel in die konjunktive Normalform überführt werden. Soll das Verfahren in polynomieller Zeit durchführbar sein, so muss man sich auf spezielle konjunktive Normalformen, auf sogenannte Horn-Klauseln einschränken.
Beispiel
Ausgangsklauseln: A∨C und B∨¬C oder - in anderer Schreibweise - Ausgangsklausel: (A∨C)∧(B∨¬C)
Resolvente: A∨B
Die Resolvente ist nicht äquivalent zu den Ausgangsklauseln. Die Ausgangsklauseln sind nur dann beide gleichzeitig erfüllbar, wenn auch die Resolvente erfüllbar ist. Die Erfüllbarkeit der Resolvente ist also eine notwendige Bedingung. Erhält man die leere Klausel ◻ als Resolvente, ist die Unerfüllbarkeit der gesamten Formelmenge gezeigt. Das ist verständlich, wenn man bedenkt, dass die Ausgangsklausel vorher so ausgesehen haben muss: (C)∧(¬C) - mit irgendeinem C.
Wahrheitstabelle zu obigem Beispiel
A B C | A∨C ¬C B∨¬C (A∨C)∧(B∨¬C) A∨B ------+--------------------------------- 0 0 0 | 0 1 1 0 0 0 0 1 | 1 0 0 0 0 0 1 0 | 0 1 1 0 1 0 1 1 | 1 0 1 1 1 1 0 0 | 1 1 1 1 1 1 0 1 | 1 0 0 0 1 1 1 0 | 1 1 1 1 1 1 1 1 | 1 0 1 1 1
mit Worten: Wenn A und B falsch sind, so ist sicher (A∨C)∧(B∨¬C) falsch, unabhängig vom Wahrheitsgehalt von C.
Aufgabe
Was ist die Resolvente zu (A∨B∨C∨D)∧(E∨¬B∨C∨F) ?
Die Antwort kann man sich auch von dem Applet von Mihai Calin Ghete geben lassen.
Beispiel eines automatischen Beweises
Folgendes Beispiel ist dem Buch 'Künstliche Intelligenz' von Lämmel und Cleve, S.47 entnommen.
Inspektor Craig hat einen Fall zu lösen. Er hat drei Personen im Verdacht, die Tat begangen zu haben. Als Täter kommen nur A, B und C in Frage. Inspektor Craig hat die Informationen:
- Wenn A schuldig und B unschuldig ist, so ist C schuldig.
- C arbeitet niemals allein.
- A arbeitet niemals mit C.
- Nur A, B oder C kommen als Täter in Frage.
Mit Hilfe der Aussagenlogik kann der Fall gelöst werden. Die aussagenlogische Variable A wird als "A war der Täter" interpretiert. Analog werden B und C interpretiert. Damit ergibt sich für den Kriminalfall diese aussagenlogische Repräsentation des Wissens:
- (A ∧ ¬B) → C
- C → (A ∨ B)
- ¬(A ∧ C)
- A ∨ B ∨ C
Es soll nun maschinell bewiesen werden, dass B der Täter ist. Das kann mit Hilfe des AL/PL-Beweisers von Lämmel und Cleve automatisch geschehen. Dazu wird folgende Text-Datei erstellt:
(a & ~b) -> c. c -> (a v b). ~(a & c). a v b v c. goal b.
Diese Text-Datei dient dann als Eingabe für den Beweiser. Der wandelt zunächst die Eingaben in die Mengenschreibweise um.
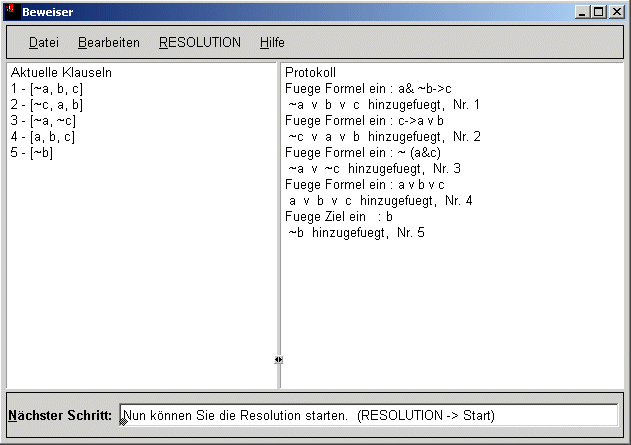
Anschließend wird mit der Resolutionsmethode ein Widerspruch gesucht.
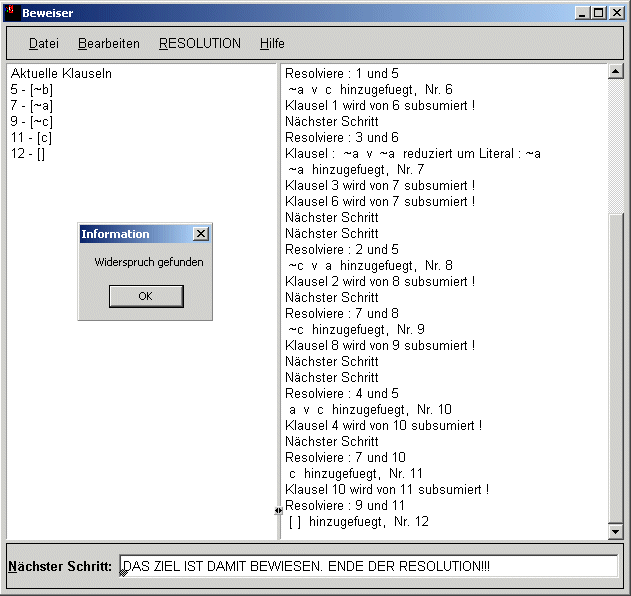
Damit ist bewiesen, dass B ein Täter war. Über eine eventuelle Mittäterschaft von A und C wurde bisher nichts ausgesagt.
Aufgabe
Leite φ1 = A∨B und φ2 = A∧B aus Φ = {A, B} her.
Die Resolutionsmethode ist nicht auf die Aussagenlogik beschränkt, sondern kann auf die Prädikatenlogik erweitert werden.
Beispiel aus der Prädikatenlogik
'Künstliche Intelligenz' von Lämmel und Cleve, S.57
Gegeben sind die Aussagen:
- Politiker mögen niemanden, der knausrig ist.
- Jeder Politiker mag eine Firma.
- Es gibt Politiker.
Es soll bewiesen werden, dass es eine Firma gibt, die nicht knausrig ist.
Die Aussagen werden in prädikatenlogische Formeln "übersetzt" und die zu beweisende Aussage negiert hinzugenommen.
- ∀ x ∀ y : poltiker(x) ∧ knausrig(y) → ¬ mag(x,y)
- ∀ x : poltiker(x) → ∃ y : firma(y)∧ mag(x,y)
- ∃ x : politiker(x)
- ¬(∃ x : firma(x) ∧ ¬ knausrig(x))
Der Beweiser kann auch PL-Probleme verarbeiten. Es ist durchaus lehrreich, sich beim Erstellen der Eingabedatei über das Setzen der Klammern genau darüber klar zu werden, was man eigentlich meint.
all(x, all(y,(politiker(x) & knausrig(y)) -> ~mag(x,y) )). all(x,politiker(x) -> ex(y,firma(y) & mag(x,y))). ex(x,politiker(x)). goal ex(x,firma(x) & ~knausrig(x)).
Zunächst werden die Klauseln in die Normalform gebracht. Das ist bei prädikatenlogischen Problemen nicht mehr ganz so einfach. Man wendet eine Methode an, die von dem norwegischen Mathematiker Albert Thoralf Skolem entwickelt wurde und ihm zu Ehren Skolemisierung heißt.
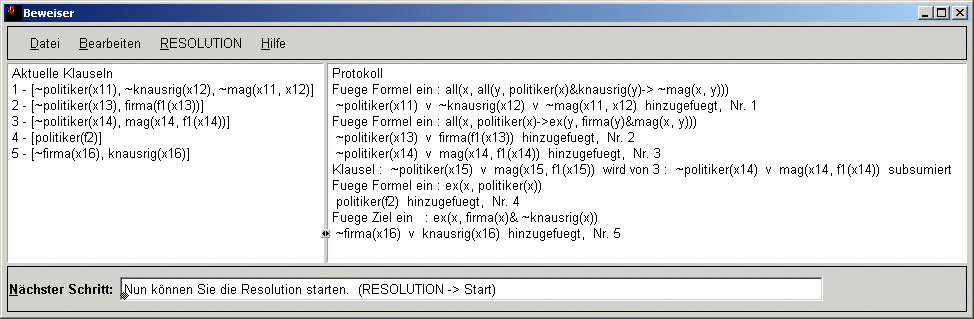
Anschließend wird mit der Resolutionsmethode ein Widerspruch gesucht.
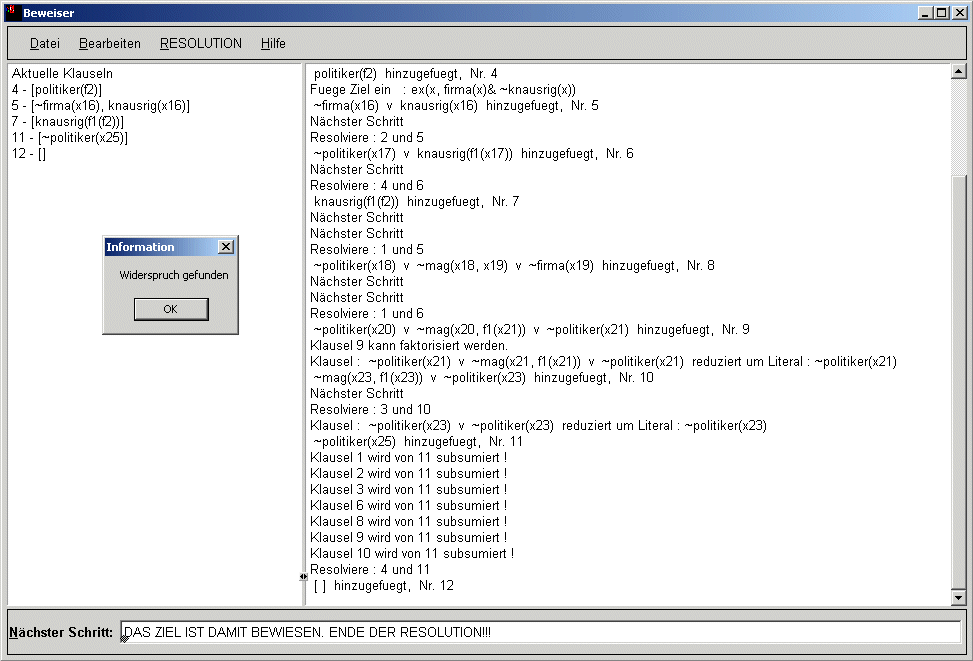
Links
- Resolution - wikipedia
- Resolution - engl. wikipedia
- Unifikation und Resolution - Prof. Peter H. Starke, HU Berlin
- Wissensverarbeitung - Zusätze zu Kapitel 2 des KI-Buches von Lämmel und Cleve
- {Re} - Das Resolutionstool von Mihai Calin Ghete
- Resolution - Tino Hempel