Unterrichtseinheit zum Satz von Pythagoras

Download der WORD-Datei (530 kB)

Klasse 9b

Hohenstaufen Gymnasium Kaiserslautern

April/Mai 1999

Gliederung:

1. Einleitung
2. Verlaufspläne
3. Arbeitsblätter
4. Folien
5. Tafelbilder

1) Einleitung:

1. Das vorliegende Unterrichtskonzept hatte als Leitideen:
1. Einführung in die Satzgruppe von Pythagoras über den Satz von Pythagoras,
2. Eigenständigkeit der Schüler,
3. Zulassen alternativer Lösungswege.
2. Nach Abwägen unterschiedlicher Zugänge (siehe Fraedrich: Die Satzgruppe von Pythagoras, Mannheim 1995 oder auch Anhang) erscheint der Zugang über den "Stuhl der Braut" (Arbeitsblatt 9) sinnvoll.
3. Da diesem Zugang eine Flächenverwandlung zu Grunde liegt, muss diese vorbereitend behandelt werden.
4. Die Motivation der Flächenverwandlung erfolgt
1. aus der innermathematischen Orientierung an der Quadratur von Figuren (siehe Arbeitsblatt 1)
2. aus dem handlungsorientierten Vorgehen, das hier möglich ist (siehe Arbeitsblatt 2, 3, 4, 5, 9)
3. aus dem Arbeiten auf verschiedenen Abstraktionsniveaus:
1. enaktive Ebene: Verwandeln durch Schneiden (s.o.),
2. ikonische Ebene: Verwandeln durch Konstruktionen ,
3. symbolische Ebene: Begründung der Konstruktionen.
5. Methodisch ergibt sich eine Notwendigkeit zur Öffnung des Unterrichts, somit (1./2., 5., 7./8. Stunde) die Gruppen- oder Partnerarbeit als sinnvolle Sozialform in wichtigen Arbeitsphasen.
6. Ergebnisse dieser Stillarbeitsphasen waren:
1. Lösungen zu den Flächenverwandlungen auf Plakate geklebt mit Lösungvarianten, zum Teil auch mit Fehlern
1. ausgeschnitten
2. als Konstruktion
2. Lösungen zum Stuhl der Braut, gesammelt auf Plakat.
3. Lösungen zu den Aufgaben im Zusammenhang mit Stuhl der Braut und Hinführung zum Satz von Pythagoras.
8. Bemerkenswerte Beobachtungen während der Unterrichtsreihe:
1. Häufig fanden Schüler vollkommen unerwartete Lösungen.
2. Durch das Zulassen von Fehlern wurde die Beweisnotwendigkeit eingesehen, manche Schülerlösungen wurden nur nach Beweis akzeptiert.
3. Günstiges Sozialverhalten beobachtbar zum Beispiel bei den Präsentationen (Diskussionen, Applaus für manche vortragende Schüler).
4. In fragend-entwickelnden Unterrichtsphasen im Anschluss an eine Schüleraktivität konnte beim dann höheren Abstraktionsniveau an den Ergebnissen der Schüler angebunden werden.
5. Schwierigkeitsgrade waren weitgehend angemessen.
6. Trotz aller Vorbereitungen wurde der wesentliche Schritt beim Stuhl der Braut nur von wenigen Schülern selbstständig gefunden.
7. Der Satz von Pythagoras ergab sich "wie von selbst".
8. Die fehlende Anwendungsorientierung wurde nicht vermisst.
9. Die täglichen Übungen konnten als Erinnerung von zur Erarbeitung wesentlichen Unterrichtsinhalten dienen (Flächeninhaltsformeln, Ähnlichkeit, usw.)

2) Verlaufspläne

9b

Klassenarbeit

3) Arbeitsblätter

Arbeitsblatt 1 und Folie 1

Arbeitsblatt 2 und Folie 2

1. Verwandle das Parallelogramm in ein flächengleiches Rechteck.
   
2. Verwandle das Rechteck in ein flächengleiches Rechteck, dessen Grundseite 1,5 mal so groß ist.
   
3. Verwandle das Parallelogramm in ein/mehrere andere flächengleiche Parallelogramme mit der gleichen Grundseite.
   
4. Verwandle das Trapez in ein flächengleiches Parallelogramm.
   




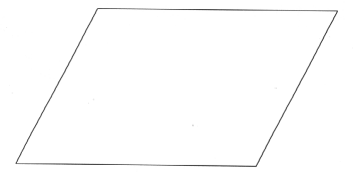
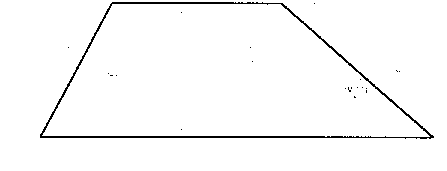
Arbeitsblatt 3 und Folie 3

5. Verwandle das Dreieck in ein Parallelogramm
   
6. Verwandle das Dreieck in ein Rechteck.
   
7. Finde ein Rechteck, dessen Flächeninhalt die Summe der Flächeninhalte der beiden Ausgangsrechtecke ist.
   
8. Verwandle das Viereck in ein flächengleiches Dreieck.
   

---

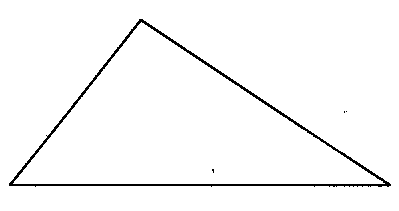
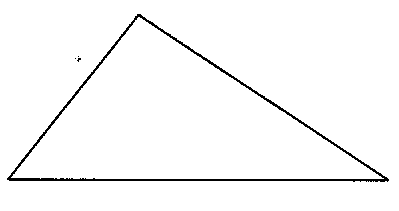
Arbeitsblatt 4 und Folie 4

9. Verwandle das Parallelogramm in ein flächengleiches Parallelogramm mit kürzerer Grundseite.
   
10. Verwandle das Dreieck in ein Dreieck, dessen Grundseite auf der gegebenen liegt, aber kürzer als diese ist.
    
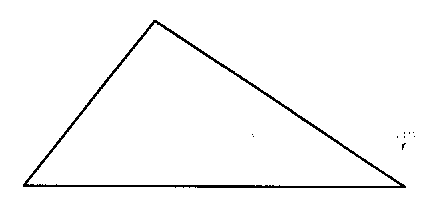
11. Finde ein Quadrat, dessen Flächeninhalt die Summe der Flächeninhalte der beiden (gleich großen) Ausgangsquadrate ist.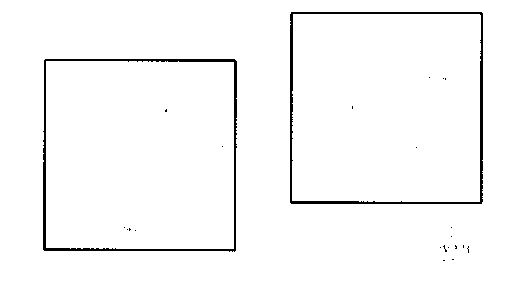
    

Arbeitsblatt 4b und Tafelbild 1

Flächenverwandlungen

Arbeitsblatt 5

Drei weitere Aufgaben zur Flächenverwandlung

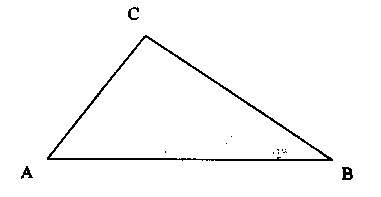
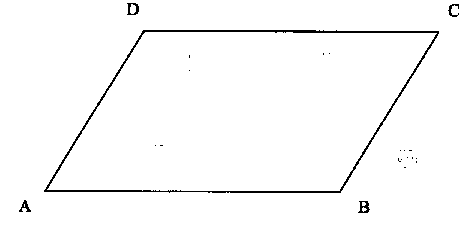
Arbeitsblatt 6 und Folie 5

Es sollen nun auch Aussagen begründet und bewiesen werden.

1. Das Parallelogramm ABCD ist in das Parallelogramm AB’FD’ flächengleich verwandelt worden.

1. Gegeben war außer dem Parallelogramm ABCD der Punkt B’. Erstelle eine Konstruktionsbeschreibung.
2. Stelle eine Verhältnisgleichung auf.
3. Ergänze die Höhen der beiden Parallelogramme, so dass sie in D bzw. D’ "enden".
4. Begründe, dass die Flächen der beiden Parallelogramme gleich sind.
5. Wieso sind auch die Flächeninhalte von B’BCE und DEFD’ gleich?

1. Das Viereck ABCD ist in das Dreieck ABC’ flächengleich verwandelt worden.
1. Gegeben war nur das Viereck ABCD. Erstelle eine Konstruktionsbeschreibung.
2. Ergänze die Höhen von Viereck und Dreieck, so dass sie in C bzw. C’ "enden".
3. Begründe, dass die Flächen der beiden Figuren gleich sind.

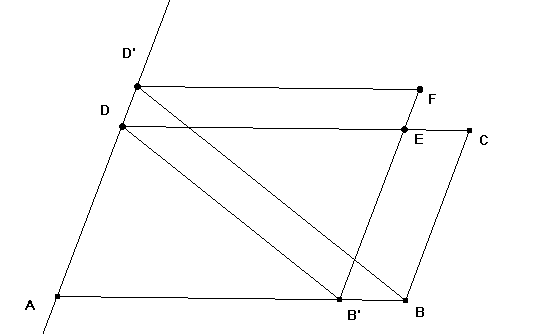
Arbeitsblatt 7 und Folie 6



2. Die beiden Quadrate ABCD und BEFC sind in das Quadrat AGEC verwandelt worden, dessen Flächeninhalt der Summe der beiden Flächeninhalte entspricht.
1. Erstelle eine Konstruktionsbeschreibung.
2. Begründe, dass der Flächeninhalt von AGEC doppelt so groß ist wie der von ABCD.
3. Nennt man die Seitenlänge eines kleinen Quadrats a und die des großen d, so gilt folgende Formel:

 

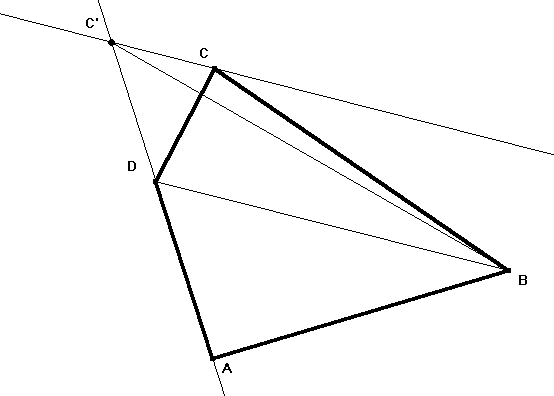
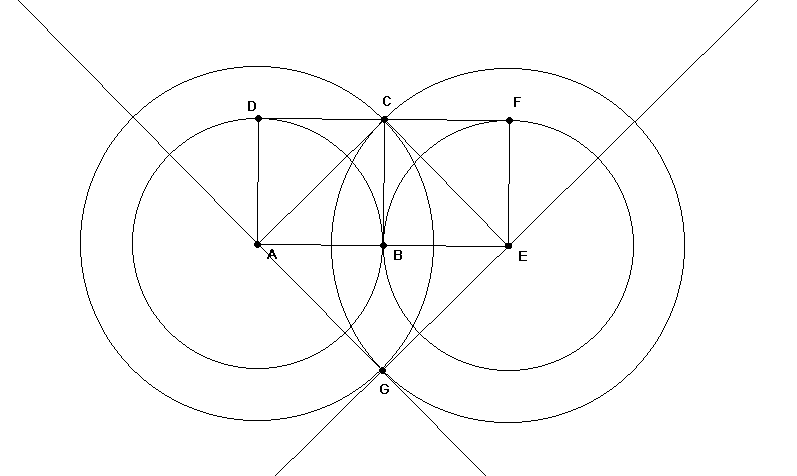4. Welche Formel für die Diagonale d eines Quadrats mit der Seitenlänge a läßt sich nun angeben:

Arbeitsblatt 8

Flächenverwandlung und Konstruktion von Längen mit irrationaler Maßzahl:

1. Zwei Quadrate mit 3cm Seitenlänge werden verwandelt in ein Quadrat, dessen Flächeninhalt der Summe der Flächeninhalte der beiden Ausgangsquadrate entspricht.
1. Wie groß ist dieser Flächeninhalt?
2. Wie lang ist eine Seite des Summenquadrats?
2. Begründe, dass sich auf diese Art mit anderen Ausgangsquadraten die Maßzahlen konstruieren lassen.
3. Um andere Maßzahlen als die in Nummer 2 zu erhalten, kann man zum Beispiel eine der folgenden Alternativen versuchen:
1. Konstruktion eines Quadrats als Summe von zwei verschiedenen Ausgangsquadraten.
2. Konstruktion eines Quadrats durch Flächenverwandlung aus einem Rechteck.
3. Konstruktion eines Quadrats durch Vergrößerung oder Verkleinerung eines gegebenen Quadrats
4. Zu den drei Möglichkeiten aus Nummer 3 erhaltet ihr Material. Es soll immer

Arbeitsblatt 9

Konstruktion eines Quadrats als Summe von zwei verschiedenen Ausgangsquadraten.

Zunächst sollt ihr die Aufgabe wieder durch Schneiden Umorientieren lösen. Später werden wir Konstruktionen nachholen.

Du hast einige Figuren zum Verschnippeln vorgegeben.

Die ersten sechs Figuren dienen der Konstruktion von Wurzel 10.

Die drei letzten Figuren dienen der Verallgemeinerung, du kannst ausprobieren, ob das Verfahren auch bei anderen Ausgangsquadraten funktioniert.

Welche Wurzeln werden bei den beiden letzten Figuren konstruiert?

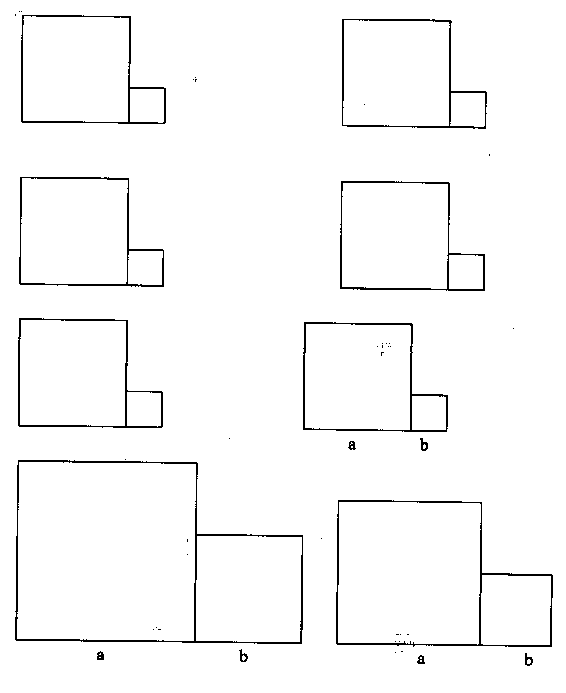
Arbeitsblatt 9b

Konstruktion eines Quadrats durch Vergrößerung oder Verkleinerung eines gegebenen Quadrats

Im Briefkuvert befinden ein kleines Quadrate mit Flächeninhalt 4 (cm²) und vier rechtwinklige Dreiecke mit den Katheten 3 (cm) und 1 (cm).

Weise nach, dass der gesamte Flächeninhalt 10 (cm²) beträgt.

Versuche, ein Quadrat zu legen.

Welche Seitenlänge hat das Quadrat?

Man kann sich auch seine Figur selbst ausschneiden:

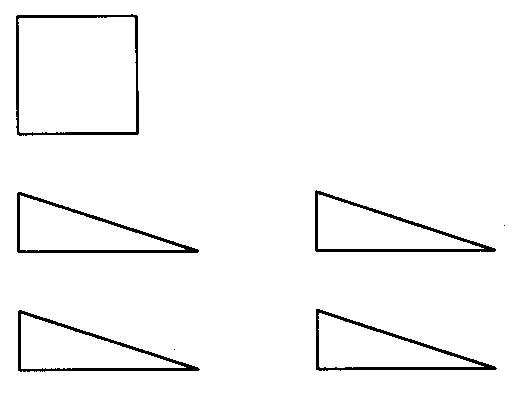
Funktioniert das auch bei anderen Grundfiguren?

Zeichne ein Ausgangsquadrat und vier (kongruente, rechtwinklige) Dreiecke und versuche es.

Ein weiterer Vorschlag:

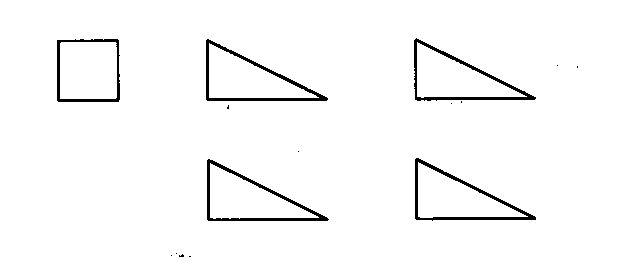
Arbeitsblatt 10 und Folie 9

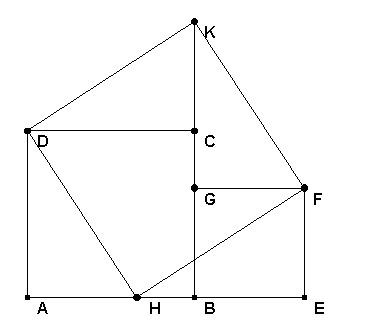
Grundfigur:

1. Leicht: Mit Hilfe der Zwei-Quadrate-Konstruktion kann man Flächeninhalte addieren und somit irrationale Maßzahlen konstruieren:
1. Um ein Quadrat mit dem Flächeninhalt 5 (cm²) zu konstruieren, kann man zwei Quadrate mit den Seitenlängen 2 und 1 addieren.
2. Konstruiere ein Quadrat mit dem Flächeninhalt 13 (cm²).
3. Konstruiere
(cm).
2. Schwer: Konstruiere ein Quadrat mit dem Flächeninhalt
1. 6 (cm²)
2. 7 (cm²)
3. 11 (cm²)
3. Schwer: Um ein Quadrat mit dem Flächeninhalt 7 (cm²) zu konstruieren, kann man entweder wie in Aufgabe 2 vorgehen, oder eine Subtraktion von Flächeninhalten versuchen. Beachte hierzu, dass gilt: (cm²). Das heißt man könnte zwei bekannte Quadrate (z.B. mit den Seitenlängen 4 (cm) und 3 (cm)) subtrahieren, um ein Quadrat zu erhalten, das den verlangten Flächeninhalt hat. Führe die Subtraktion zeichnerisch durch:
1. Zeichne das größere Quadrat (in der Grundfigur HFKD)
2. Versuche, das Quadrat ABCD zu finden. Konstruiere hierzu den Punkt A in der Grundfigur (mit Zirkel und Lineal).
4. Leicht: Verschiebt/spiegelt man in der Grundfigur die kleinen Quadrate, erhält man die folgende Figur:

Arbeitsblatt 11

Aufgaben zum Satz von Pythagoras

1. Mit Hilfe des Satzes von Pythagoras kann man "Quadrate addieren, subtrahieren, multiplizieren und dividieren".

Gegeben sind zwei Quadrate Q₁ und Q₂ mit den Seitenlängen a und b.

1. Zeichne ein Quadrat, dessen Flächeninhalt gleich der Summe der Flächeninhalte der beiden Quadrate ist.
2. Zeichne ein Quadrat, dessen Flächeninhalt gleich der Differenz der Flächeninhalte der beiden Quadrate ist.
3. Zeichne ein Quadrat, dessen Flächeninhalt gleich dem doppelten Flächeninhalt von Q₁ ist.
4. Zeichne ein Quadrat, dessen Flächeninhalt gleich dem fünffachen Flächeninhalt von Q₁ ist.
5. Zeichne ein Quadrat, dessen Flächeninhalt gleich drittel Flächeninhalt von Q₁ ist.
2. Zeige: In jedem Rechteck ist die Summe der Quadrate über den vier Seiten gleich dem doppelten Quadrat über der Diagonalen.
3. Das gleichschenklige Giebeldreieck eines 36m langen und 24m breiten Hauses ist 5m hoch. Berechne die Größe der überall mit den Wänden abschließenden Dachfläche.
4. Gesucht ist die Höhe eines Giebeldreiecks, dessen Grundlinie 8m und dessen Schenkel 5m lang sind.
5. Bei einem Brückenbogen ist AB die Spannweite, CD die Bogenhöhe. Suche eine Beziehung zwischen Spannweite, Bogenhöhe und Radius r.
6. Ein Fußweg auf einen Berg verläuft zwischen A (Höhenlinie 310) und B (Höhenlinie 325) geradezu geradlinig. Die Entfernung AB beträgt nach der Karte 250m.

Arbeitsblatt 12

Aufgaben zum Satz von Pythagoras

7. Suche auf einer Straßenkarte im Bergland eine Straße mit großer Steigung. Wähle eine kleine, geradezu geradlinige Straße aus. Zeichne das Profil der Straße (Horizontalmaßstab 1:10000, Vertikalmaßstab 1:100). Bestimme Steigung und wahre Länge.
8. Bestimme die Entfernung zweier unzugänglicher Punkte A, B. Erkläre das Verfahren.
   
9. Bestimme den Radius des kleinsten Kreises eines romanischen Fensters , wenn die Breite des Fensters (Kämpferlinie) b ist.



10. Bestimme jeweils x:
    

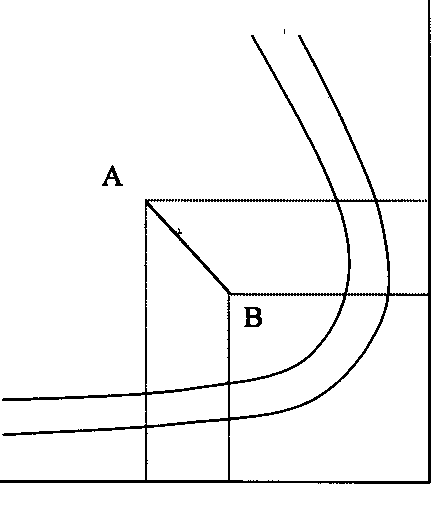
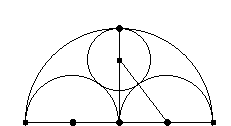
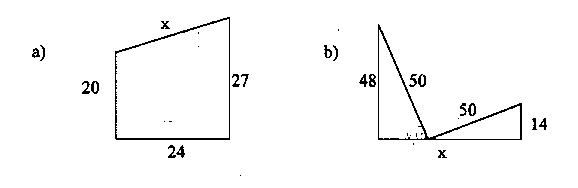
4) (fehlende) Folien

Folie 7

Folie 8

Gruppenarbeit und Präsentation

1. Durchführung der Stillarbeit
1. Versucht, das Problem lösen
2. Diskutiert Lösungmöglichkeiten
3. Arbeitet mit den Gruppenmitgliedern/dem Partner zusammen
4. Kommunikation ist erwünscht, stört aber nicht die anderen Schüler (und den Lehrer)
2. Vorbereitung der Präsentation während der Stillarbeit
1. Stellt das Problem/die Aufgabe dar
2. Dokumentiert die Lösung
1. verständlich
2. fachlich präzise
3. vollständig
3. Wählt die Präsentationsmedien
1. Plakat
2. Folie
3. Tafel
4. andere
4. Achtet auf die äußere Gestaltung
1. Veranschaulichungen
2. Schriftgröße
3. Farben
3. Durchführung der Präsentation
1. Auswahl der Präsentierenden
1. Los
2. nach Wahl der Schüler
3. nach Wahl des Lehrers
4. Andere Kriterien
2. Stellt das Thema heraus
3. Macht eine Gliederung deutlich
4. Teilt die Zeit gut ein
5. Achtet auf deine Körpersprache und auf Blickkontakt
6. Nachfragen der Mitschüler sind erwünscht
4. Nach der Präsentation
1. Bewertung der Präsentation
1. informell
2. mit Note für einzelne
3. mit Note für die Gruppe

5) Tafelbild

Tafelbild 2

Bezeichne a=AB, b=BF

Konstruktion:

Wähle H so, dass .

Dann gilt .

Zeichne HF, HD.

Zeichne "die" Orthogonale zu HF durch F.

Zeichne "die" Orthogonale zu HD durch D.

Den Schnittpunkt der beiden Orthogonalen bezeichne mit K.

Behauptung: Die Konstruktion liefert ein Quadrat und es gilt .

Beweis:

Die Dreiecke AHD und HEF sind kongruent nach Kongruenzsatz sws, weil....

Also gilt .

, weil...

Also ist HFKD ein Quadrat.

Die Dreiecke AHD und DCK sowie HFG und KFG sind nach Kongruenzsatz Ssw kongruent.

Subtrahiere ich von der Gesamtfigur die Dreiecke DCK und KGF, so erhalte ich als Rest .

Subtrahiere ich von der Gesamtfigur die Dreiecke AHD und HEF, so erhalte ich als Rest . Also sind diese beiden Flächen gleich. q.e.d.