Unterrichtsreihe zum Satz des Pythagoras HSG KL (Schenkel) Mai 1999
Download der WORD-Datei (145 kB)
Unterrichtsreihe zur Einführung des Satzes des Pythagoras
( Hohenstaufen-Gymnasium Kaiserslautern , Mai 1999 )
Grobkonzept:
- In diesem Konzept werden zunächst mit einem geschlossenen Knotenseil ,
einer zeichnerisch-experimentellen Phase und selbstgebastelten Knoten-
schnüren pythagoreische Zahlentripel aufgestellt.
Die Beschreibung der pythagoreischen Zahlentripel führt zur Formulierung
der Umkehrung des Satzes des Pythagoras. Diese Umkehrung wird zunächst
als Satz vom Knotenseil bezeichnet.
- Nach einem Einschub über logische Aussagen soll die Einsicht gewonnen
werden, dass die Umkehrung einer Folgerung ( eines Satzes ) im allgemeinen
nicht immer wahr sein muss , d.h. dass Umkehrungen
bewiesen werden müssen.
- Nun wird die Umkehrung des Satzes vom Knotenseil formuliert und
als Satz des Pythagoras bezeichnet. ( Die Notwendigkeit des Beweises
sollte den Schülern nach dem Einschub über logische Aussagen klar sein ).
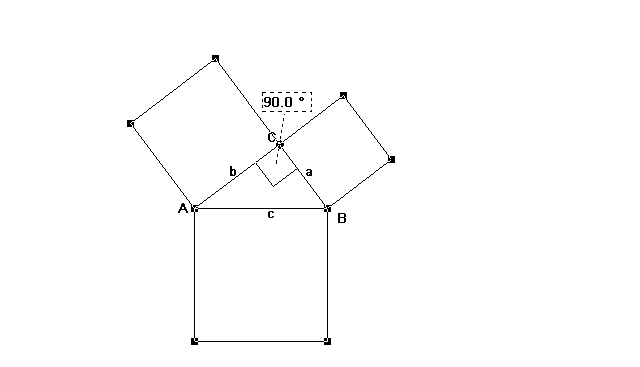
Die Formulierung des Satzes wird zunächst durch eine Pythagorasfigur
( rechtwinkliges Dreieck mit den beiden Kathetenquadraten und
dem Hypotenusenquadrat ) veranschaulicht.
Pythagorasfigur

- Die Prinzipien von Zerlegungs- und Ergänzungsbeweis werden mit den
Schülern besprochen.
- Der Satz des Pythagoras soll mit Hilfe eines Ergänzungsbeweises bewiesen
werden. Dies soll in Gruppenarbeit durch Zerschneiden der Pythagorasfigur,
Ausschneiden von weiteren Flächen und Zusammensetzen der beiden
Ergänzungsfiguren geschehen.
( Es wird der Impuls gegeben , in der Pythagorasfigur entlang der
Hypotenuse zu schneiden, so dass einerseits das Hypotenusenquadrat entsteht,
andererseits das rechtwinklige Dreieck mit den beiden Kathetenquadraten.
( Die beiden Kathetenquadrate sind also schon um das zugehörige
rechtwinklige Dreieck ergänzt. )
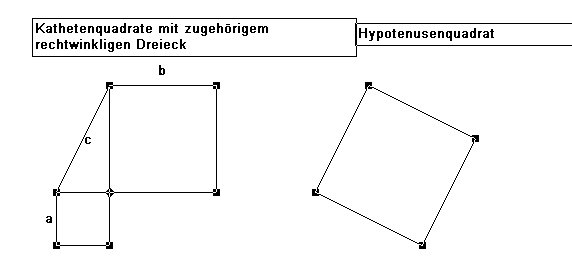
Die beiden Kathetenquadrate und das Hypotenusenquadrat sollen jeweils
durch kongruente Figuren ergänzt werden, so dass jeweils die entstehenden
Ergänzungsfiguren kongruent zueinander sind .
( Prinzip des Ergänzungsbeweises ! )
)
Ergänzungsfigur 1
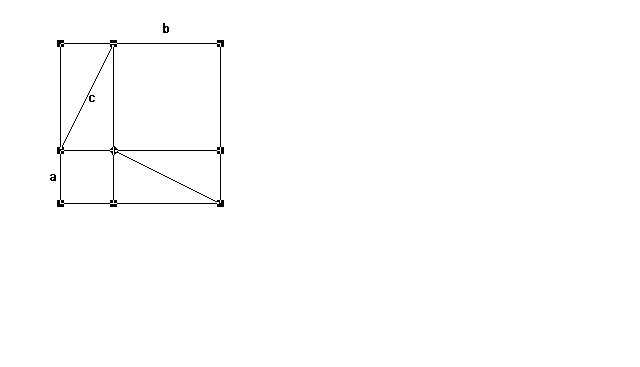
Ergänzungsfigur 2
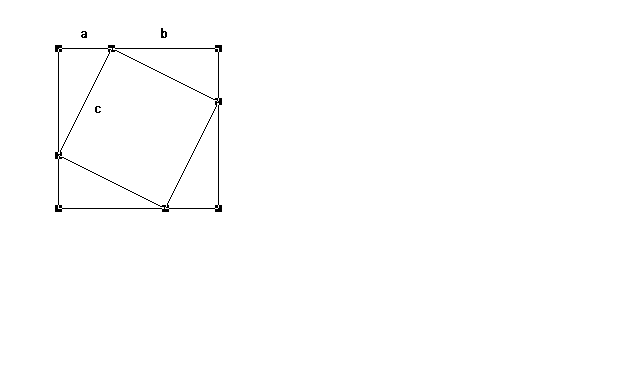 ( Literatur: (1) Peter Baptist, Pythagoras und kein Ende ?
( Literatur: (1) Peter Baptist, Pythagoras und kein Ende ?
(2) A.M. Fraedrich, Die Satzgruppe des Pythagoras )
1. Stunde:
-Den Schülern wird das Titelbild des Buches "Das Geheimnis des Orion"
( von Robert Bauval / Adrian Gilbert ) mit den drei deutlich sichtbaren
Pyramiden von Gizeh gezeigt. Es wird kurz angesprochen, dass in der
großen Pyramide (Cheops-Pyramide) in den letzten Jahren Schächte
entdeckt wurden, die auf bestimmte Sternbilder zeigen.Unter anderem,
dass im südlichen Schacht der Königinkammer mit Hilfe des fahrbaren
Roboters UPUAUT 2 (mit Videokamera) eine bis heute noch nicht
geöffnete kleine Tür entdeckt wurde.
Im Schüler-Lehrer-Gespräch wurde der Bau der regelmäßigen vier-
seitigen Pyramiden von Gizeh ( quadratische Grundfläche )
angesprochen, unter anderem die Vermessung der rechten Winkel
der Grundflächen der Pyramiden.
Zu der Vermessung von rechten Winkeln im alten Ägypten wurde eine
Folie auf dem Overhead-Projektor mit einem altägyptischen Motiv
gezeigt, das sogenannte Seilspanner mit einem Knotenseil und den
zugehörigen Spannpflöcken erkennen lässt.
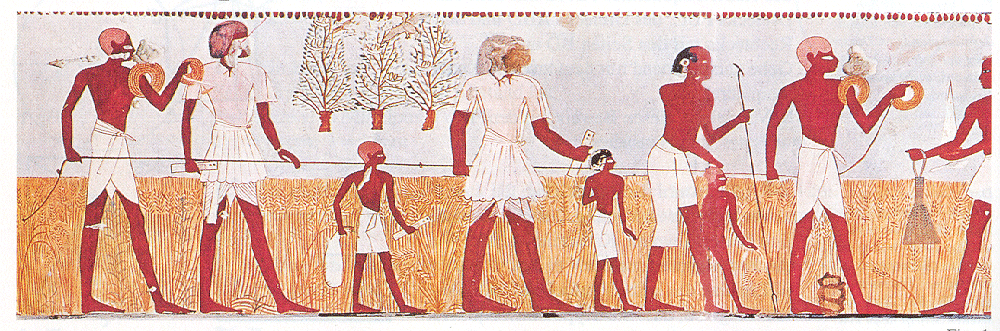
-Ich hatte mir bei der Vorbereitung der Unterrichtsreihe in einem
Baumarkt ein (grünes) Seglerseil gekauft und damit ein geschlossenes
Knotenseil mit 12 Längeneinheiten geknüpft ( 1LE = 60cm ).
Die Gesamtlänge des ( geschlossenen ) Knotenseils war so gewählt, dass
drei Schüler im Klassensaal einen rechten Winkel aufspannen können.
-Problemstellung: Erzeugen eines rechten Winkels mit Hilfe eines
geschlossenen Knotenseils mit 12 Längeneinheiten,
wobei das Knotenseil an 3 Stellen gespannt wird.
-Drei Schüler versuchten dies experimentell im Klassensaal. Die erzeugten
Winkel wurden mit dem rechten Winkel eines Schülertisches verglichen.
Zunächst wurden folgende Zahlentripel erzeugt, bei denen kein
rechter Winkel entstand: (4, 4, 4), (5, 5, 2) .
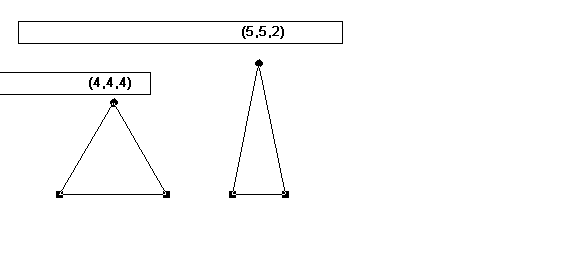
Dann wurde experimentell das pythagoreische Zahlentripel (3, 4, 5)
gefunden, das deutlich einen rechten Winkel zeigt ( im Gegensatz zu
den obigen Zahlentripeln ) .
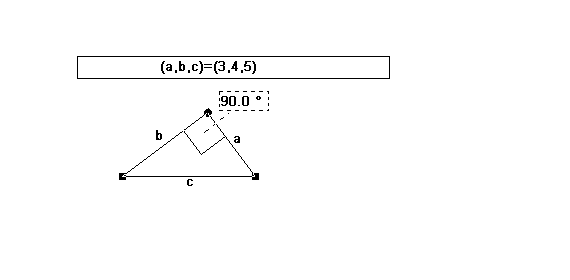
- Zur Sicherung wird unter der Überschrift "Pythagoreische Zahlentripel"
das experimentell gefundene Zahlentripel an der Tafel und im Heft
festgehalten und das zugehörige rechtwinklige Dreieck mit Zirkel und
Lineal konstruiert.Dabei werden die Begriffe Kathete und Hypotenuse
wiederholt und gefestigt.
- Zum systematischen Suchen von weiteren pythagoreischen Zahlentripeln
wird nun an der Tafel und im Heft auf kariertem Untergrund
ein rechter Winkel in die linke obere Ecke der Zeichenebene gezeichnet
und die Katheten ( in der Horizontalen a,
in der Vertikalen nach unten b )
mit Längeneinheiten versehen ( 1LE = 0,5 cm = 1Knotenabstand ) .
( Rechtwinkliges Suchdiagramm (siehe 2. Stunde) )
- Ganzzahlige Hypotenusen sollen nun zeichnerisch-experimentell zu
ganzzahligen Katheten gefunden werden.
- Als erstes wird die Hypotenuse c = 5 aus dem pyth. Zahlentripel
(3, 4, 5) eingezeichnet.
- In einer experimentellen Phase werden nun neu entdeckte ganzzahlige
Hypotenusen von den Schülern an der Tafel eingezeichnet und
das zugehörige pyth. Zahlentripel festgehalten.
- Die gefundenen Lösungen werden von allen Schülern ins Heft
übernommen.
- Die Schüler entdecken, dass weitere ganzzahlige Hypotenusen
( mit den zugeh. pyth. Zahlentripel ) parallel zu der Hypotenuse c = 5
des pyth. Z-trip. (3, 4, 5) liegen.
Dieses Ergebnis wird an der Tafel und im Heft festgehalten.
- Zwei Schüler haben jedoch gegen Ende der Stunde außerdem
das pyth. Zahlentripel (12, 5, 13) entdeckt, dessen Hypotenuse c = 13 in dem rechtwinkligen Suchdiagramm nicht parallel zu der Hypotenuse c = 5
des pyth. Z-trip. (3, 4, 5) liegt. ( Es wird die Vermutung ausgesprochen,
dass es noch weitere pyth. Z-trip. gibt, deren Hypotenusen in dem
rechtwinkligen Suchdiagramm nicht parallel zu c = 5 liegen. )
- Hausaufgabe: 1.) Finden von weiteren pythagoreischen Zahlentripeln
mit Hilfe des rechtwinkligen Suchdiagramms
( Einzeichnen der Lösungen )
2.) Basteln einer geschlossenen Knotenschnur zu
einem pyth. Zahlentripel
2. Stunde:
- Zu Beginn der Stunde können die Schüler die Funktionstüchtigkeit ihrer
selbsgeknüpften geschlossenen ( z.T. farbigen ) Knotenschnüre vorführen.
Die meisten Schüler haben Knotenschnüre zu dem pyth. Zahlentripel (3, 4, 5)
gebastelt, einige wenige haben aufwendigere Knotenschnüre zu dem
pyth. Zahlentripel (6, 8, 10) geknüpft.
- Während dieser Phase zeichnet ein Schüler das rechtwinklige Suchdiagramm
mit den in der letzten Stunde gefundenen ganzzahligen Hypotenusen an die
Tafel und hält auch die dazugehörigen pyth. Zahlentripel an der Tafel fest.
( Anmerkung: Bei einer nochmaligen Durchführung dieser Unterrichtsreihe
würde ich das rechtwinklige Suchdiagramm mit den ganz-
zahligen Hypotenusen auf einer Overhead-Folie festhalten. )
- Nun werden von den Schülern weitere in der Hausaufgabe gefundene
ganzzahlige Hypotenusen an der Tafel eingezeichnet und die zugehörigen
pyth. Zahlentripel angeschrieben.
Die Schüler ergänzen gleichzeitig das rechtwinklige Suchdiagramm in
ihrem Heft und entsprechend ihre pyth. Zahlentripel.
Rechtwinkliges Suchdiagramm zum systematischen Finden
von pythagoreischen Zahlentripeln
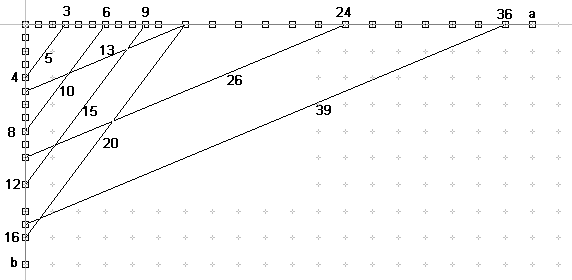
- Die Schüler erkennen, dass bisher zwei Gruppen von pythagoreischen
Zahlentripeln gefunden wurden.
Eine Gruppe1, deren Hypotenusen in dem rechtwinkligen Suchdiagramm
parallel zu der Hypotenuse c = 5 des pyth. Z-trip. (3, 4, 5) liegen.
Eine Gruppe2, deren Hypotenusen in dem rechtwinkligen Suchdiagramm
parallel zu der Hypotenuse c = 13 des pyth. Z-trip. (12, 5, 13) liegen.
- Die bisher gefundenen pyth. Z.-trip. werden in diese zwei Gruppen
getrennt an der Tafel und im Heft notiert.
Gruppe1 Gruppe2
( a, b, c) ( a, b, c)
( 3, 4, 5) (12, 5,13)
( 6, 8,10) (24,10,26)
( 9,12,15) (36,15,39)
(12,16,20)
- Es ergibt sich im Schüler-Lehrer-Gespräch folgende Problemstellung:
Es wird eine mathematische Beschreibung für die gefundenen
pythagoreischen Zahlentripel gesucht.
- Dabei verständigen sich die Schüler darauf, zunächst eine Beschreibung
für die beiden gefundenen Gruppen getrennt aufzustellen.
Eine geometrische Beschreibung über die Lage der Hypotenusen
innerhalb einer Gruppe ( im rechtwinkligen Suchdiagramm) war ja
schon gefunden worden ( Parallelität der Hypotenusen).
Es ging also darum, eine algebraische Beziehung unter den pyth.
Z-trip. jeweils einer Gruppe zu finden.
1. Versuch:
Gruppe1
( a, b, c)
(3, 4, 5 ) = ( 3, 3+ 1, 3+ 2)
(6, 8,10) = (2*3,2*3+2*1,2*3+2*2)
(9,12,15) = (3*3,3*3+3*1,3*3+3*2)
(12,16,20)=(4*3,4*3+4*1,4*3+4*2)
( a, b, c)=(k*3,k*3 +k*1,k*3+k*2) mit ![]()
( a, b, c)=(k*3,k*4,k*5) mit ![]()
- Die Schüler haben zunächst die Beziehungen zwischen den
Katheten a und die wachsenden Differenzen b-a und c-a
berücksichtigt. Zum Schluss stellte sich dann heraus, dass es
einfacher ist, die Tripel der Gruppe1 als Vielfache des pyth. Z-trip.
( 3, 4, 5 ) darzustellen
Die Schüler erkannten nun auch, dass die rechtwinkligen Dreiecke,
die den pyth. Z-trip. der Gruppe1 zu Grunde liegen, durch zentrische
Streckung mit dem ganzzahligen Streckfaktor ![]() und dem
und dem
Streckzentrum C aus dem Dreieck mit den Seitenlängen ( 3, 4, 5)
hervorgehen .
- Die Erkenntnise, die bei der Beschreibung der Gruppe1 gewonnen
wurden, werden analog auf die pyth. Z-trip derGruppe2
übertragen.
Folgendes Ergebnis wird an der Tafel und im Heft festgehalten:
Beschreibung der pyth. Zahlentripel der Gruppe 1:
Man erhält alle pyth. Zahlentripel der Gruppe 1 als Vielfache
des Tripels ( 3, 4, 5) :
( k*3, k*4, k*5) mit ![]() .
.
Die zu den pyth. Z-trip. gehörigen rechtwinkligen Dreiecke
gehen durch zentrische Streckung mit dem ganzzahligen
Streckfaktor ![]() ( und dem Streckzentrum C ) aus dem
( und dem Streckzentrum C ) aus dem
Dreieck mit den Seitenlängen ( 3, 4, 5) hervor.
( Die Hypotenusen der Dreiecke der Gruppe1 liegen
( im rechtwinkl. Suchdiagr. ) parallel zueinander. )
Beschreibung der pyth. Zahlentripel der Gruppe2:
Kurzform:
( k*12, k*5, k*13) mit ![]()
( Die Hypotenusen der Dreiecke der Gruppe2 liegen
( im rechtwinkl. Suchdiagr. ) parallel zueinander. )
Unterrichtsreihe zum Satz des Pythagoras HSG KL (Schenkel) Mai 1999
- Nachdem eine getrennte mathematische Beschreibung für die
gefundenen pyth. Zahlentripeln der Gruppe1 und Gruppe2 formuliert
ist, steht noch immer eine gemeinsame Beschreibung aus.
- Ein Schüler macht dazu den Vorschlag, man solle doch mal die
Quadrate der Zahlen in den pyth. Zahlentripeln betrachten.
Da dieser Vorschlag gegen Ende der Stunde gemacht wird, führt
dies zu folgender Hausaufgabe:
1.) Aufstellen der quadratischen Zahlentripel zu den
pyth. Zahlentripeln ( aus Gruppe1 und Gruppe2 )
2.) Zusammenhang zwischen den Quadraten
der Zahlen aus den pyth. Z-trip. herausfinden
3.Stunde:
- Tafelanschrieb der quadratischen Zahlentripel zu den
pyth. Zahlentripeln ( aus Gruppe1 und Gruppe2 )
durch einen Schüler
Gruppe1 Gruppe2
![]()
![]()
( 9 ,16, 25) (144, 25,169)
(36,64,100) (576,100,676)
(81,144,225) (1296,225,1521)
(144,256,400)
- Die Schüler haben schon in der Hausaufgabe erkannt, dass für
alle pyth. Zahlentripel gilt: ![]()
( Festhalten dieses Ergebnisses )
- Diese Erkenntnis wird bezogen auf Dreiecke folgendermaßen
formuliert:
Vermutung zum Knotenseil:
Gilt für die Seiten eines Dreiecks ![]() ,
,
dann hat das Dreieck bei C einen rechten Winkel ( ![]() ) .
) .
Kurzschreibweise:
Aus ![]() .
.
- Es stellt sich nun die Frage, gilt auch die Umkehrung der
Vermutung zum Knotenseil ?
- Um diese Frage zu klären, wird ein kleiner Exkurs in die
Aussagenlogik unternommen.
- Es werden z.B. folgende Aussagen betrachtet:
A: Dies ist ein Pudel
B: Dies ist ein Hund
Es gilt: Aus ![]() , denn ein Pudel ist immer auch ein Hund .
, denn ein Pudel ist immer auch ein Hund .
Es gilt jedoch nicht: Aus ![]() , denn ein Hund muss nicht
, denn ein Hund muss nicht
immer ein Pudel sein.
- Die Schüler gewinnen die Einsicht, dass die Umkehrung einer
Folgerung im allgemeinen nicht wahr sein muss.
- Die Umkehrung der Vermutung zum Knotenseil muss also bewiesen
werden.
- Die Umkehrung der Vermutung zum Knotenseil (Satz des Pythagoras)
wird zunächst in Kurzschreibweise formuliert.
Aussage A : ![]()
Aussage B : ![]()
Vermutung zum Kotenseil: Aus ![]()
![]()
Umkehrung der Vermutung zum Knotenseil
( Satz des Pythagoras ) : Aus ![]()
![]()
- Die ausführliche Formulierung des Satzes des Pythagoras und
der Beweis sind für die nächste Stunde geplant.
- Hausaufgabe: Bilden von 5 (sprachlichen) Folgerungen und iher
Umkehrungen ( Testen des jeweiligen Wahrheitswertes)
4./5. Stunde (Doppelstunde):
- Zunächst werden die Folgerungen und ihre Umkehrungen
der Hausaufgabe besprochen.
Dabei wird nochmals die Notwendigkeit des Beweises des Satzes
des Pythagoras betont.
- Da in der letzten Stunde der Satz des Pythagoras nur in der Kurz-
schreibweise vorlag, soll er nun ausführlich formuliert
werden und seine Geltung als Flächensatz durch eine Zeichnung
( Pythagorasfigur ) veranschaulicht werden.
Satz des Pythagoras:
In jedem rechtwinkligen Dreieck haben die Quadrate über
den Katheten zusammen den gleichen Flächeninhalt wie
das Quadrat über der Hypotenuse.
Anders ausgedrückt: Sind in einem rechtwinkligen Dreieck a und b
die Kathetenlängen und c die Hypotenusenlänge,
so gilt: ![]() .
.
Kurzschreibweise: Aus ![]()
Pythagorasfigur
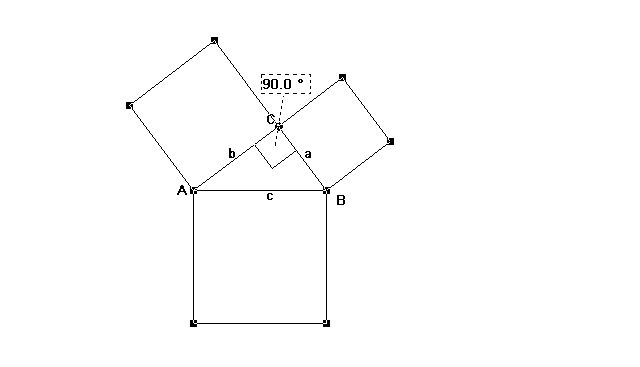
- Die Prinzipien von Zerlegungs- und Eegänzungsbeweis werden
mit den Schülern besprochen.
- Der Satz des Pythagoras soll mit Hilfe eines Ergänzungsbeweises
bewiesen werden.Dies soll in Gruppenarbeit geschehen.
- Die Schüler haben für diese Stunde Scheren und, Klebestifte mitgebracht.
Jede Gruppe (3-4 Schüler) erhält einen Bogen weißen Pappkarton
und farbiges Papier zum Ausschneiden und Aufkleben. Außerdem
erhält jede Gruppe eine Folie und einenFolienstift, um die Ergebnisse
auf der Folie festzuhalten.
Ein oder zwei Schüler sollen zum Schluss die Ergebnisse mit Hilfe
der Folie am Overhead-Projektor vorstellen (Pythagorasfigur und
die beiden erarbeiteten Ergänzungsfiguren).
Die schönsten aufgeklebten Ergänzungsfiguren sollen im Klassen-
zimmer aufgehängt werden.
- Die Pythagorasfigur wird auf das farbige Papier gezeichnet.
Die Pythagorasfigur soll so zerschnitten werden, dass durch
Ausschneiden von weiteren Flächen und Zusammensetzen dieser
Flächen mit den passenden Teilen der Pythagorasfigur die beiden
Ergänzungsfiguren entstehen.
( Es wird der Impuls gegeben, in der Pythagorasfigur entlang der
Hypotenuse zu schneiden, so dass einerseits das Hypotenusenquadrat
entsteht, andererseits das rechtwinklige Dreieck mit den beiden
Kathetenquadraten. ( Die beiden Kathetenquadrate sind also schon
um das zugehörige rechtwinklige Dreieck ergänzt. )
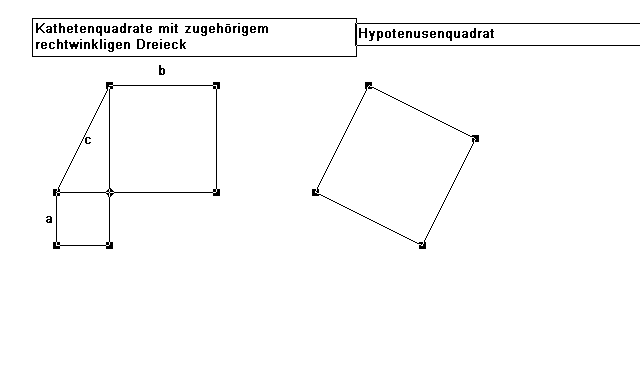
Die beiden Kathetenquadrate und das Hypotenusenquadrat sollen jeweils
durch kongruente Figuren ergänzt werden, so dass jeweils die entstehenden
Ergänzungs figuren kongruent zueinander sind.
( Prinzip des Ergänzungsbeweises ! )
)
Ergänzungsfigur 1 Ergänzungsfigur 2
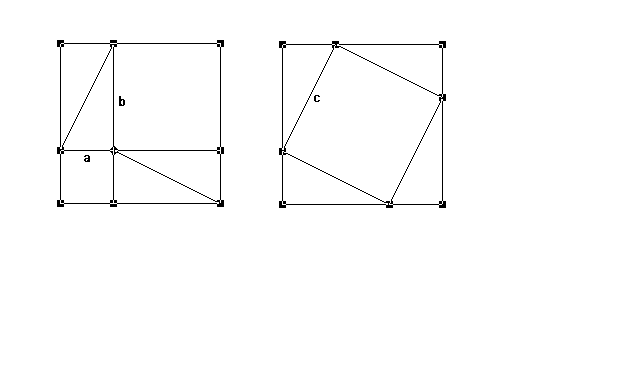
- Die Ergänzungsfigur 1 wurde relativ schnell in den einzelnen
Gruppen gefunden.
- Obwohl bei der Ergänzungsfigur 2 die Form schon durch die
Ergänzungsfig. 1 bekannt war, wurde in den Gruppen länger
über die Lage des Hypotenusenquadrats und die Ergänzungsdreiecke
diskutiert.
- Die Ergänzungsfigur 1 haben in der Stunde alle Gruppen
gefunden. Die Ergänzungsfigur 2 haben 4 von 5 Gruppen gefunden.
- Zwei Gruppen schildern mit Hilfe ihrer Folie am Overheadprojektor
wie sie ihre Ergänzungsfiguren gefunden haben.
- Die beiden Ergänzungsfiguren werden dann von allen Schülern
ins Heft übernommen.
- Die schönsten mit dem Farbpapier zusammengeklebten
Ergänzungsfiguren 1 und 2 werden im Klassenzimmer aufgehängt,
um die Beweisidee des gewählten Beweises während der Unter-
richttsreihe der Satzgruppe des Pythagoras jederzeit sichtbar
zu haben.
Hausaufgabe:( Anwendung des Satzes des Pythagoras )
Berechne den Flächeninhalt des gleichschenkligen
Dreiecks mit den Seiten a=13; b=13; c=10.
( Planfigur! Rechnung! )
(Tip: Zeichne in der Planfigur die Höhe auf die Basis ein! )