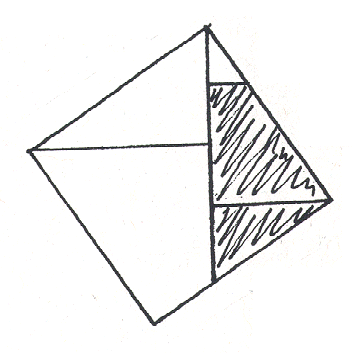
Alle Teildreiecke sind rechtwinklig-
gleichschenklig und zueinander kongruent.
Deshalb ist das entstehende Viereck ein
Rechteck mit gleichlangen Seiten,
also ein Quadrat.
Unterrichtsreihe zur Einführung des Satzes des Pythagoras
1. Stunde
Problemstellung (Arbeitsblatt 1, Tafel; Unterrichtsgespräch (UG); 10min) Das Tischdeckenproblem| TdP 1 | geg.: Zwei Quadrate mit dem Flächeninhalt a2 |
| ges.: Quadrat mit dem Flächeninhalt A=2a2 | |
| TdP 2 | geg.: Zwei Quadrate der Flächeninhalte a2 und b2 |
| ges.: Quadrat mit dem Flächeninhalt A = a2 + b2 |
Begründung:
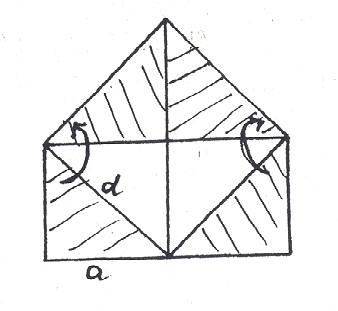
| Alle Teildreiecke sind rechtwinklig- gleichschenklig und zueinander kongruent. Deshalb ist das entstehende Viereck ein Rechteck mit gleichlangen Seiten, also ein Quadrat. |
 |
Satz 1
Das Quadrat über der Diagonalen d eines Quadrates der Kantenlänge a hat einen Flächeninhalt, der doppelt so groß ist wie derjenige des Ausgangsquadrates:
d2 = 2a2
Folgerung: Für die Diagonale eine Quadrates mit der Seite a gilt: ![]() .
.
Hausaufgabe: siehe Beispiel 1 (Anlage)
2. Stunde
Besprechung der Hausaufgabe (s. Anlage)
Lösen der Teilaufgabe b)
Lösung zu b)
Unterrichtsgespräch
Tischdeckenproblem b)
geg.: Quadrate mit den Seiten a und b; ![]()
ges.: Quadrat mit A = a2 + b2
1. Versuch:
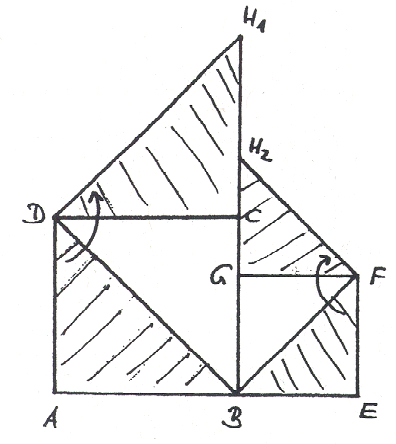 |
Ziel: H1 = H2 Schüler zerschneiden Papierquadrate Idee: Wähle statt B einen Punkt X ÎAB |
2. Versuch:
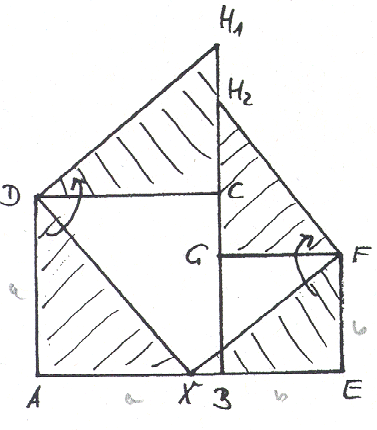 |
H1 ist Bildpunkt von X bei einer Drehung um 90° von D
AXD um D. ==> H2 ist Bildpunkt von X bei einer Drehung um 90° von D
XEF um F. ==> Daher gilt H1 = H2 nur dann, wenn
Mit folgt daraus:
Und damit gilt |
Hausaufgabe:
Konstruiere X für a = 3 cm und b = 2 cm.
Zeige, dass das Viereck DXFH1(H2) ein Quadrat ist (Winkel(FXD) = 90° und ![]() ).
).
3. Stunde
Zusammenfassung der Hausaufgabe
Ergebnis:
Konstruktion:
1. Trage b in A an AB ab, man erhält X
2. Ergänze DX und XF zu einem Rechteck
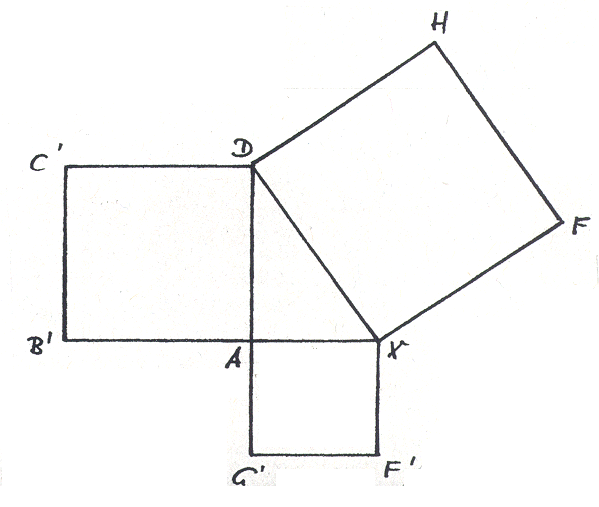
Behauptung: Viereck DXFH ist ein Quadrat
Beweis:
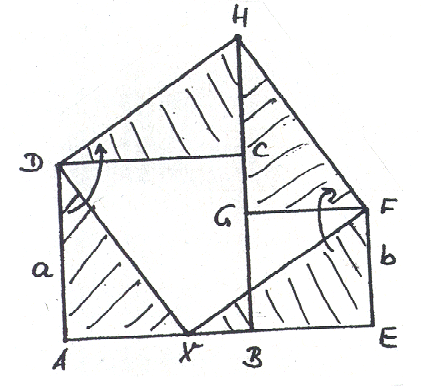 |
1. Die Dreiecke D AXD und D XEF sind wegen sws kongruent ==> 2. D AXD ist rechtwinklig ==> Winkel(ADX) + Winkel(DXA) = 90° und wegen Winkel(EXF) = Winkel(ADX) folgt daraus Winkel(FXD) = 90°. Aus 1. und 2. folgt, dass das Viereck DXFH ein Quadrat ist. |
Die Schüler zerschneiden zwei verschiedenfarbige Papierquadrate mit ![]() und kleben die Teile in Form eines Quadrates mit A = a2 + b2 ins Heft.
und kleben die Teile in Form eines Quadrates mit A = a2 + b2 ins Heft.
Die neue Tischdecke
Übergang zur "Pythagorasfigur" durch "Ausklappen" der Kathetenquadrate.
Aus obigem Beweis ergibt sich der berühmte Satz des Pythagoras
| In jedem rechtwinkligen Dreieck ist die Summe der Flächeninhalte der Quadrate über den Katheten gleich dem Flächeninhalt des Quadrats über der Hypotenuse. In mathematischer Kurzschreibweise: D ABC rechtwinklig mit der Hypotenuse c ==> a2 + b2 = c2 Hausaufgabe: Puzzleteile einmal zu zwei Quadraten und einmal zu einem Quadrat zusammensetzen. Beide Konfigurationen in Form der Pythagorasfigur ins Heft zeichenen (Vom Lehrer vorbereitete Puzzles zu weiteren Zerlegungsbeweisen) 4. Stunde Die Schüler erhalten ein Arbeitsblatt mit den Lösungen der Hausaufgabe. Besprechung der Lösungen in Bezug auf das Tischdeckenproblem. Besprechung der Lösungen in Bezug auf den Satz des Pythagoras. Übungen zum Satz des Pythagoras |
 |