 |
|||
| HSG |
|
Lemma von Bachet
Für je zwei natürliche Zahlen a und b gibt es ganze Zahlen x und y mit ggT(a,b) = x·a+y·b.
Beispiel
ggT(1001,203) = 7 und 7 = 14·1001−69·203
Python
Die Quelle für diesen Algorithmus findet sich auf der Seite www.algorithmist.com.
def eggt(a,b):
"""
gibt für a,b >= 0 ein Tripel (g,x,y) zurueck, für das gilt ax + by = g = ggT(a,b)
"""
if b == 0:
return (a,1,0)
else:
print(a,'=',a//b,'*',b,'+',a%b) # DEBUG
(g,x,y) = eggt(b,a%b)
print(g,y,x -(a//b)*y) # DEBUG
return (g,y,x -(a//b)*y)
def modinv(a, m):
"""
gibt das modulare Inverse zu a und dem Modul m zurück
"""
g, x, y = eggt(a, m)
if g != 1:
return None
else:
return x % m
Beispiel
An einem Beispiel soll das Vorgehen und die Benennungen geklärt werden.
a b a//b a%b Gleichung ----------------------------------------------------- 42 76 0 42 42 = 0 * 76 + 42 76 42 1 34 76 = 1 * 42 + 34 42 34 1 8 42 = 1 * 34 + 8 34 8 4 2 34 = 4 * 8 + 2 8 2 4 0 8 = 4 * 2 + 0 2 0
Der Algorithmus terminiert, wenn b zu 0 geworden ist. Benennt man a zu a0 und b zu a1 um, so kann man den Algorithmus als das rekursive Erzeugen einer Folge von ai auffassen.
a b a//b a%b ------------------------------- a0 a1 a0//a1 a0%a1 a1 a2 a1//a2 a1%a2 a2 a3 a2//a3 a2%a3 a3 a4 a3//a4 a3%a4 a4 a5 a4//a5 a4%a5 a5 a6In der Notation des Beweises zum Euklidischen Algorithmus ist hier n = 5 und damit a5 = g der gesuchte ggT und a6 = 0. Der ggT taucht also als 'Rest' mit der Nummer 5 auf. Es gilt nun aber die Rekursiongleichung \[ \text{(1) } \; a_i = a_{i-2} - q \cdot a_{i-1} \text{ mit } q = a_{i-2}//a_{i-1} \] Im Algorithmus wird q jeweils durch a//b dargestellt. Es soll nun der ggT g durch eine Linearkombination zweier aufeinanderfolgender Reste dargestellt werden. \[ g = y \cdot a_{i+1} + x \cdot a_{i} \] dabei ist x der Koeffizient des älteren Restes. Für i = n kann man die Koeffizienten wegen an = g berechnen: x = 1 und y = 0 \[ g = 0 \cdot a_{n+1} + 1 \cdot a_{n} \] Setzt man jetzt (1) in (2) \[ \text{(2) } \; g = y \cdot a_{i} + x \cdot a_{i-1} \] ein, so erhält man \[ \text{(3) } \; g = y \cdot (a_{i-2} - q \cdot a_{i-1}) + x \cdot a_{i-1} = (x - q \cdot y) \cdot a_{i-1} + y \cdot a_{i-2}\] An der Gleichung kann man die Beziehungen \[ x_{neu} = y_{alt} \] und \[ y_{neu} = x_{alt} -q \cdot y_{alt}\] ablesen. Obiger Algorithmus berechnet also im 'Hinabsteigen' den ggT und im 'Hinaufsteigen' die Koeffizienten x und y. Ganz schön raffiniert!
Beispiel
>>> eggt(1001,203) 1001 = 4 * 203 + 189 203 = 1 * 189 + 14 189 = 13 * 14 + 7 14 = 2 * 7 + 0 7 0 1 7 1 -13 7 -13 14 7 14 -69 (7, 14, -69) >>> 14*1001-69*203 7
Das (multiplikative) modulare Inverse zu a modulo m
Man weiß aus dem Vorangehenden, dass das Inverse genau dann existiert, wenn \( (a,m) = 1 \) gilt. Nach dem Lemma von Bachet gibt es aber ganze Zahlen x und y mit \[ 1 = (a,m) = x \cdot a + y \cdot m \] Das bedeutet aber, dass x das modulare Inverse ist \[ x \cdot a \equiv 1(m) \] x%m bildet man, um einen Repräsentanten zwischen 0 und m zu bekommen.
Beispiel
>>> a = 24 >>> m = 37 >>> eggt(a,m) 24 = 0 * 37 + 24 37 = 1 * 24 + 13 24 = 1 * 13 + 11 13 = 1 * 11 + 2 11 = 5 * 2 + 1 2 = 2 * 1 + 0 1 0 1 1 1 -5 1 -5 6 1 6 -11 1 -11 17 1 17 -11 (1, 17, -11) >>> i=17 >>> a*i 408 >>> (a*i)%m 1
Aufgabe
Suche dir zwei richtig große Zahlen a und m mit (a,m) = 1, bestimme das modulare Inverse und teste die Eigenschaft.
Ein Krypto-System mit modularer Multiplikation
Zuerst wählt man sich ein Modul n, z.B. n = 2571234567890257. Jetzt wählt man sich einen 'öffentlichen Schlüssel' e (encrypt), z.B. e = 17. Ist n eine Primzahl, haben alle 'Reste' ein Inverses, kommen also als 'öffentlicher Schlüssel' e (encrypt) in Frage. Falls n keine Primzahl ist, muss man (e,n) = 1 überprüfen, denn nur unter diese Bedingung findet man ein modulares Inverses d (decrypt). Es interessant, die Rechenzeiten zur Primzahlfaktorzerlegung, ggt und modularem Inversen zu vergleichen. Auch ohne Messungen erlebt man ggt und modinv als effizient und primfaktoren als langsam. Bitte mit krypto0.py ausprobieren.
>>> n = 2571234567890257 >>> e = 17 >>> ggt(n,e) 1 >>> primfaktoren(n) [29, 107, 828628607119] >>> >>> d = modinv(e,n) >>> d 453747276686516 >>> e*d%n 1 >>>
Aus einer Botschaft 'HSG' macht man zunächst durch eine geeignete Codierung eine Bytefolge b. Aus dieser Bytefolge errechnet man dann eine große ganze Zahl m (message). Diese Zahl muss kleiner als das Modul n sein, daher auch die Beschränkung auf eine kurze Botschaft. Was macht man, wenn die Botschaft länger sein soll?
>>> b = bytes('HSG','utf8')
>>> b
b'HSG'
>>> m = bton(b)
>>> m
4739911
>>> m < n
True
In der eigentlichen Verschlüsselung wird aus der 'Klartextzahl' m mit Hilfe des 'öffentlichen Schlüssels' (e,n) eine 'Chiffratzahl' c errechnet. Man beachte, dass der öffentliche Schlüssel aus zwei Zahlen besteht. Ein Detail am Rande: '*' bindet stärker als '%', sodass (m*e)%n zu m*e%n gleich ist.
>>> c = m*e%n >>> c 80578487 >>> c < n True
Das Chiffrat c kann mit Hilfe des 'geheimen Schlüssels' (d,n) wieder entschlüsselt werden. Es entsteht zuerst eine Zahl m1, die mit ntob wieder zu einer Bytefolge gemacht werden muss.
>>> m1 = c*d%n >>> m1 4739911 >>> b1 = ntob(m1) >>> b1 bytearray(b'HSG') >>> str(b1,'utf8') 'HSG'
Warum funktioniert das?
(m*e)*d%n = m*(e*d)%n = m*1%n = m
Das Problem
Wie vorgeführt funktioniert ein asymmetrisches Kryptosystem basierend auf modularer Multiplikation ganz prima. Trotzdem besteht ein gravierendes Problem. Welches?
Aufgabe
Spiele wie oben ein asymmetrisches Kryptosystem basierend auf modularer Addition durch. Hat so ein System die Chance, sich durchzusetzen?
Delphi
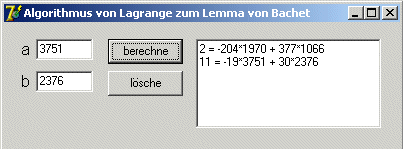
// Herrmann, Algorithmen Arbeitsbuch, S.138
procedure Lagrange(a,b : int64; var x,y,ggt : int64);
var
q,r,t,u,v : integer;
begin
x := 0; y := 1;
u := 1; v := 0;
q := a div b; r := a mod b;
while r > 0 do
begin
a := b; b := r;
t := u; u := x; x := t-q*x;
t := v; v := y; y := t-q*y;
q := a div b; r := a mod b;
end;
ggt := b;
end;
zu einem 'Hand-Algorithmus'
Modulares Inverses
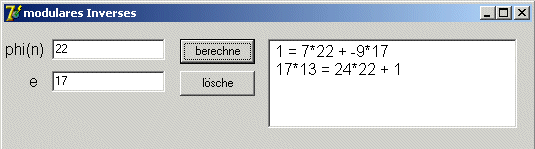
begin
phiN := StrToInt(ePhiN.text); e := StrToInt(eE.text);
Lagrange(phiN,e,x,y,g);
if y < 0
then
begin
d := phiN+y; k := x+e; // entspricht Addition von e*phi(n)
end
else
begin
d := y; k := -x;
end;
s := IntToStr(g)+' = '+IntToStr(x)+'*'+IntToStr(phiN)+' + '+
IntToStr(y)+'*'+IntToStr(e);
mAusgabe.Lines.Add(s);
s := IntToStr(e)+'*'+IntToStr(d)+' = '+IntToStr(k)+'*'+IntToStr(phiN)+' + '+
IntToStr(g);
mAusgabe.Lines.Add(s);
end;