 |
|||
| HSG |
|
Der Satz von Euler
Beispiel
Zu n = 15 ist r = [1, 2, 4, 7, 8, 11, 13, 14] ein reduziertes Restesystem. a = 22 ist zu n = 15 teilerfremd.
>>> n = 15 >>> r = [x for x in range(n) if ggt(x,n)==1] >>> r [1, 2, 4, 7, 8, 11, 13, 14] >>> phin = len(r) >>> phin 8 >>> a = 22 >>> r1 = [x*a%n for x in r] >>> r1 [7, 14, 13, 4, 11, 2, 1, 8]
Vermutlich überrascht es nicht sehr, dass das Produkt der Zahlen aus r gleich dem Produkt der Zahlen aus r1 ist. Es sind schließlich die gleichen Zahlen nur in anderer Reihenfolge.
>>> 1*2*4*7*8*11*13*14 896896 >>> import functools # für reduce >>> import operator # für mul >>> P = functools.reduce(operator.mul,r,1) >>> P 896896 >>> P1 = functools.reduce(operator.mul,r1,1) >>> P1 896896 >>> P == P1 True
P1 kann man aber durch φ(n)-maliges Ausklammern von a als aφ(n) P schreiben. P ist als Produkt von zu n teilerfremden Zahlen selbst zu n teilerfremd. Daher kann man die Kongruenz aφ(n) P ≡ P (n) durch P kürzen.
>>> ggt(P,n) 1 >>> ((a**phin)%n*P)%n == P%n True >>> (a**phin)%n 1 >>>
Zusammengefasst: Wenn (a,n) = 1 gilt, so folgt aφ(n)%n = 1 bzw. aφ(n) ≡ 1 (n).
Aufgabe 1
Vollziehe die Rechnungen des Beispiels für selbstgewählte Zahlen n und a mit (a,n) = 1 nach. Die Zahlen dürfen ruhig etwas größer sein.
Aufgabe 2
Verwende krypto.py und berechne für mindestens 10 teilerfremde Zahlenpaare m und den Ausdruck mφ(n) mod n. Was fällt auf?
>>> m=27 >>> n=35 >>> ggt(m,n) 1 >>> modpower(m,phi(n),n) 1 >>> m=4321 >>> n=1234 >>> ggt(m,n) 1 >>> modpower(m,phi(n),n) 1 >>>
'Roadmap' zum Satz von Euler
- Definition: a ≡ b mod m ⇔ a ≡ b (m) ⇔ m|(a-b) (Definition Teilbarkeit)
- Satz: a ≡ b (m) ⇒ ac ≡ bc (m)
- Satz: ac ≡ bc (m) ⇒ a ≡ b (m/(c,m)) ( (c,m) = ggT(c,m) )
- Definition: Ein System von Zahlen ar, die zu einem gegebenen Modul m teilerfremd
( (ar,m) = 1 ) und paarweise modulo m inkongruent ("verschiedene Reste" ) sind, heißt
reduziertes Restesystem.
Beispiel: Modul m = 10, reduziertes Restesystem: 1, 3, 7, 9 - Definition: Die Anzahl der zu m teilerfremden Zahlen 1,2,...,m (das reduzierte Restesystem) heißt φ(m) (Eulersche Funktion).
- Satz: (k,m) = 1 und a1,a2,...,am vollständiges (alle Reste kommen vor) Restesystem ⇒ ka1,ka2,...,kam ist vollständiges Restesystem
- Satz: (k,m) = 1 und a1,a2,...,aφ(m) reduziertes Restesystem ⇒ ka1,ka2,...,kaφ(m) ist reduziertes Restesystem
- Satz von Euler: (a,m) = 1 ⇒ aφ(m) ≡ 1(m)
- Folgerung: Satz von Fermat: (a,p) = 1, p Primzahl ⇒ ap-1 ≡ 1(p)
Satz 6, Der Satz von Euler
(a,m) = 1 ⇒ aφ(m) ≡ 1(m)
Beweis: Aus dem bezüglich m reduzierten Restesystem a1, a2, ..., aφ(m) wird das Produkt P1 a1⋅a2⋅ ...⋅aφ(m) gebildet. Nach Satz 5 ist auch a⋅a1, a⋅a2, ..., a⋅aφ(m) ein reduziertes Restesystem. Auch aus diesem Restesystem wird ein Produkt P2 a⋅a1⋅a⋅a2⋅ ...a⋅aφ(m) gebildet. Die beiden Restesysteme enthalten modulo m die gleichen Reste, sodass P1 ≡ P2 (m) gilt. In P2 klammert man nun aφ(m) aus, sodass nun P1 ≡ aφ(m) ⋅ P1 gilt. P1 ist aber als Produkt zu m teilerfremder Zahlen selbst zu m teilerfremd. Jetzt kann man daher nach Satz 2 durch P1 'kürzen'. Es bleibt die Kongruenz 1 ≡ aφ(m) stehen, das ist die Behauptung.∎
Satz 7, Der Satz von Fermat
p Primzahl, (a,p) = 1 ⇒ ap-1 ≡ 1(p)
Beweis: Der Satz folgt aus dem Satz von Euler, wenn man φ(p) = p-1 bedenkt. Das wiederum gilt, weil eine Primzahl p zu allen Zahlen a, 1 ≤ a < p teilerfremd ist. ∎
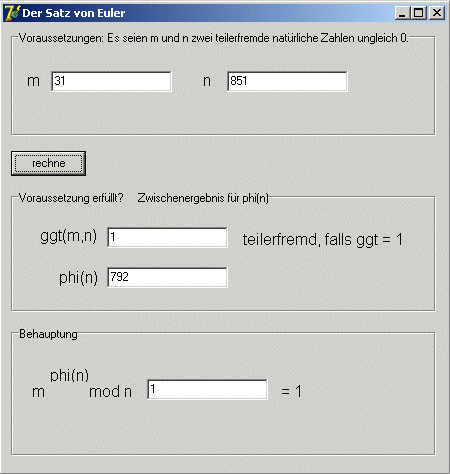
Links
- Eulersche φ-Funktion - wikipedia
- Beweis des kleinen Satzes von Fermat - Arndt Brünner