 |
|||
| HSG |
|
L = {anbn|n aus IN} ist nicht regulär
Es sollen hier Erläuterungen und Ergänzungen zu dem Beweis aus Seite 147/148 aus Gasper/Leiß/Stimm/Spengler, Technische und theoretische Informatik gegeben werden. Dh. die folgende Notation hält sich bewusst an die Vorlage.Angenommen, es gibt doch einen endlichen Automaten A mit L(A) = L, so hat er eine feste Anzahl Zustände, etwa m = 15 (natürlich kann er viel, viel mehr haben, das spielt aber für das Beweisprinzip keine Rolle). Wie wählen uns nun ein Wort aMbM aus L(A) mit M > m, etwa M=16.
Bei der Abarbeitung des Wortes a16b16 muss bereits bei der Verarbeitung der 16 a's mindestens ein Zustand Z zweimal durchlaufen werden, denn es gibt mehr a's als Zustände. Die genannten Autoren nehmen ohne Beschränkung der Allgemeinheit (o.B.d.A.) an, dass der Zustand, der mit dem dritten a erreicht wird, mit dem siebten a wiederum erreicht wird. Das heißt aber, dass eine Schleife entstanden ist, die erst mit dem ersten b wieder verlassen wird. Wie die 16 b's den Automaten in einen Endzustand bringen, ist für den Beweis ohne Belang. Eine mögliche Konstellation zeigt das folgende Bild:
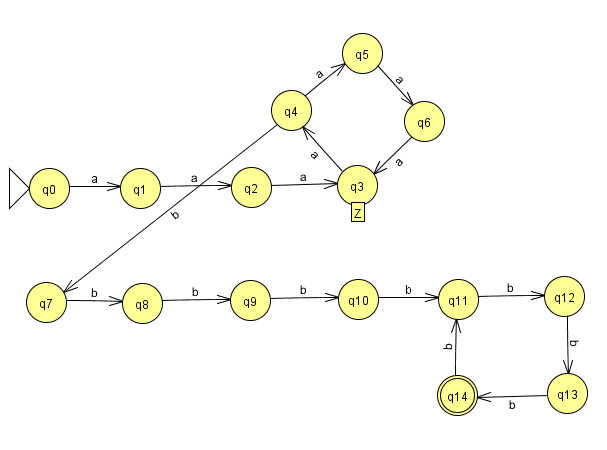 glss147.jff
glss147.jffMan entnimmt dem Bild, dass natürlich auch a4b16 (Schleife wurde nicht durchlaufen) oder auch a8b16 (Schleife wurde einmal durchlaufen) akzeptiert werden. Der Automat akzeptiert also auch Worte außerhalb von L.
Das ist ein Widerspruch!