Transformation Welt —› Bild

Ein Grundproblem der Grafik-Programmierung ist die Transformation sogenannter Welt-Koordinaten (x/y) auf Bildschirm-Koordinaten (u/v). Im Folgenden soll anhand eines Beispiels die Entwicklung der Transformation gezeigt werden: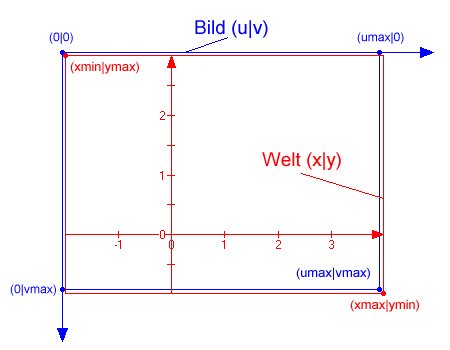

Ansatz

u = a*x + b
v = c*y + d
gesucht: Koeffizienten a, b, c, d

Gleichungen

Welt	Bild
(xmin/ymax)	(0/0)
(xmax/ymin)	(umax/vmax)


=>	I	0 = a*xmin + b	II	0 = c*ymax + d
=>	III	umax = a*xmax + b	IV	vmax = c*ymin + d

Lösungen

III - I:
umax - 0 = a(xmax - xmin) => a = umax/(xmax-xmin)
a in I:
b = - a*xmin
IV - II:
vmax - 0 = c(ymin - ymax) => c = vmax/(ymin-ymax)
c in II:
d = - c*ymax

Kleines Demo-Programm

Klassendiagramm

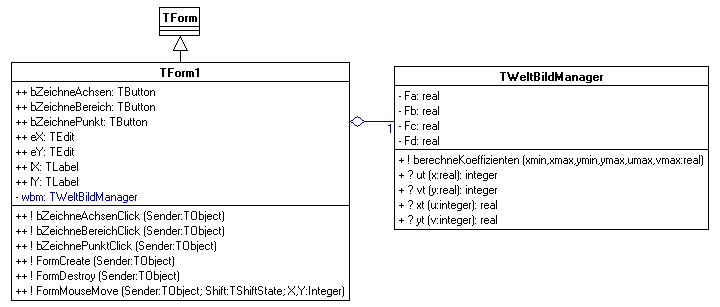mTWeltBildManager.zip
Zur Demonstration des Vorstehenden soll ein kleines Programm entwickelt werden. Wir machen einen Welt-Bild-Manager für die Transformationen verantwortlich. Dazu muss dieser die Koeffizienten Fa,Fb,Fc,Fd abspeichern. Diese Koeffizienten müssen vor dem Zeichnen berechnet werden. Das macht die Methode berechneKoeffizienten, der die nötigen Parameter übergeben werden. Schließlich braucht man die transformierten Werte, die von Funktionen, wie z.B. ut (u-transformiert) geliefert werden. ut und vt erledigen auch gleich die nötigen Rundungen, da das Bild-System ganze Zahlen erwartet.

Programm-Details

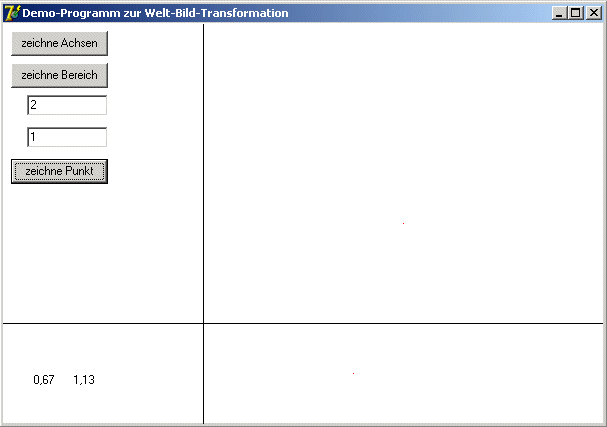
Das Programm benutzt die Transformationen in beiden Richtungen:
zum Zeichnen von Weltpunkten (x/y) im Bild (ut(x)/vt(y))
zum Anzeigen der Mauskoordinaten (u/v) in der Welt (xt(u)/yt(v))

Es ist zu beachten, dass für eine unverzerrte Darstellung das gleiche Verhältnis von Breite : Höhe in Welt und Bild erforderlich ist.

Quelltext-Auszüge aus der Unit mTWeltBildManager

.......
procedure TWeltBildManager.berechneKoeffizienten(xmin,xmax,ymin,ymax,umax,vmax : real);
begin
  Fa := umax/(xmax-xmin); Fb := -Fa*xmin;
  Fc := vmax/(ymin-ymax); Fd := -Fc*ymax;
end;

function TWeltBildManager.ut(x : real) : integer;
begin
  result := round(Fa*x+Fb);
end;
.........
function TWeltBildManager.xt(u : integer) : real;
begin
  result := (u - Fb)/Fa;
end;
........

Quelltext-Auszüge aus der Formular-Unit:

........
procedure TForm1.FormCreate(Sender: TObject);
begin
  wbm := TWeltBildManager.Create;
  wbm.berechneKoeffizienten(-2,4,-1,3,600,400);
end;
........
procedure TForm1.bZeichneAchsenClick(Sender: TObject);
begin
  with canvas do
  with wbm do
  begin
    // x-Achse
    MoveTo(ut(-2),vt(0)); LineTo(ut(+4),vt(0));
    // y-Achse
    MoveTo(ut(0),vt(-1)); LineTo(ut(0),vt(3));
  end;
end;
.......
procedure TForm1.FormMouseMove(Sender: TObject; Shift: TShiftState; X,
  Y: Integer);
var
  u,v : integer;
begin
  u := x; v := y;
  with canvas do
  with wbm do
  begin
    TextOut(ut(-1.7),vt(-0.5),'        ');        // Leerstring zum Löschen
    TextOut(ut(-1.7),vt(-0.5),FloatToStr(xt(u))); // neuer Text
    TextOut(ut(-1.3),vt(-0.5),'        ');
    TextOut(ut(-1.3),vt(-0.5),FloatToStr(yt(v)));
  end;
end;

Downloads

Transformation.zip
mTWeltBildManager.zip

Aufgaben

Erweitere das Programm um
- Graph einer Funktion, z.B. Gf mit f(x) = 0.2*x²-0.5 im Bereich [-1;3]
- kleine Striche auf den Achsen
- Beschriftung der Striche
- Pfeile an den Achsen
- Rasterpunkte
- ....