Lemma von Bachet (DIFF,CM1,S.30)
Für je zwei natürliche Zahlen a und b gibt es ganze Zahlen x und y mit ggT(a,b)=x*a+y*b.
Beispiel
| | | | | | |
|
| | | | | | 0 |
|
| | | | | | 1 |
| |
| 1001 | = | 4 | * | 203 | + | 189 |
|
| | | | | | 1 |
|
| | | | | | -4 |
| 189=1*1001-4*203 |
| 203 | = | 1 | * | 189 |
+ | 14 |
|
0 | - | 1 | * | 1 | = |
-1 |
|
1 | - | 1 | * | -4 | = | 5 |
| 14=-1*1001+5*203 |
| 189 | = | 13 | * | 14 |
+ | 7 | |
1 | - | 13 | * | (-1) | = |
14 | |
-4 | - | 13 | * | 5 | = |
-69 |
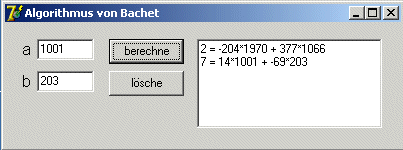
| 7=14*1001-69*203 |
| 14 | = | 2 | * | 7 | + |
0 |
|
| | | | | |
| |
| | | | | |
|
| |
Der Algorithmus erweitert den gewöhnlichen Algorithmus von Euklid um die Berechnung der
Koeffizienten
xi und
yi zur Darstellung des jeweiligen Restes.
Dabei gelten die rekursiven Gleichungen
x
i = x
i-2-c
i*x
i-1 und
y
i = y
i-2-c
i*y
i-1.
Die x
i-1 bzw. x
i-2 (y
i-1 bzw. y
i-2) findet man
dabei in der gleichen Spalte 1 oder 2 Zeilen darüber, c
i ist der
ganzzahlige Quotient in
der gleichen Zeile im Euklid-Schema. Wenn man will, so kann man - wie oben in der letzten Spalte
geschehen - die Darstellung der Reste fortlaufend kontrollieren.
weiteres Beispiel
| | | | | | |
|
| | | | | | 0 |
|
| | | | | | 1 |
| |
| 1970 | = | 1 | * | 1066 | + | 904 |
|
| | | | | | 1 |
|
| | | | | | -1 |
| 904=1*1970-1*1066 |
| 1066 | = | 1 | * | 904 | + | 162 |
|
0 | - | 1 | * | 1 | = |
-1 | |
1 | - | 1 | * | (-1) | = |
2 |
| 162=-1*1970+2*1066 |
| 904 | = | 5 | * | 162 | + | 94 |
|
1 | - | 5 | * | (-1) | = |
6 | |
-1 | - | 5 | * | 2 | = |
-11 |
| 94=6*1970-11*1066 |
162 | = | 1 | * | 94 | + | 68 |
|
-1 | - | 1 | * | 6 | = |
-7 | |
2 | - | 1 | * | (-11) | = |
13 |
| 68=-7*1970+13*1066 |
| 94 | = | 1 | * | 68 | + | 26 |
|
6 | - | 1 | * | (-7) | = |
13 | |
-11 | - | 1 | * | 13 | = |
-24 |
| 26=13*1970-24*1066 |
| 68 | = | 2 | * | 26 | + | 16 |
|
-7 | - | 2 | * | 13 | = |
-33 | |
13 | - | 2 | * | (-24) | = |
61 |
| 16=-33*1970+61*1066 |
| 26 | = | 1 | * | 16 | + | 10 |
|
13 | - | 1 | * | (-33) | = |
46 | |
-24 | - | 1 | * | 61 | = |
-85 |
| 10=46*1970-85*1066 |
16 | = | 1 | * | 10 | + | 6 |
|
-33 | - | 1 | * | 46 | = |
-79 | |
61 | - | 1 | * | (-85) | = |
146 |
| 6=-79*1970+146*1066 |
| 10 | = | 1 | * | 6 | + | 4 |
|
46 | - | 1 | * | (-79) | = |
125 | |
-85 | - | 1 | * | 146 | = |
-231 |
| 4=125*1970-231*1066 |
| 6 | = | 1 | * | 4 | + | 2 |
|
-79 | - | 1 | * | 125 | = |
-204 | |
146 | - | 1 | * | (-231) | = |
377 |
| 2=-204*1970+377*1066 |
| 4 | = | 2 | * | 2 | + |
0 |
|
| | | | | |
| |
| | | | | |
|
| |
Delphi-Programm
Bachet.zip
// DIFF CM1 Algorithmen der elementaren Zahlentheorie, S.32
procedure Bachet(a,b : integer; var g,x,y : integer);
var
bg,bu,cg,cu,xg,xu,yg,yu : integer;
begin
bg := a; cg := 0; xg := 1; yg := 0;
bu := b; cu := a div b; xu := 0; yu := 1;
while (bg <> 0) and (bu <> 0) do
begin
xg := xg-cu*xu; yg := yg-cu*yu; bg := bg mod bu;
if bg = 0
then
begin
g := bu; x := xu; y := yu;
end
else
begin
cg := bu div bg; xu := xu-cg*xg;
yu := yu-cg*yg; bu := bu mod bg;
end;
if bu = 0
then
begin
g := bg; x := xg; y := yg;
end
else
cu := bg div bu;
end;
end;
