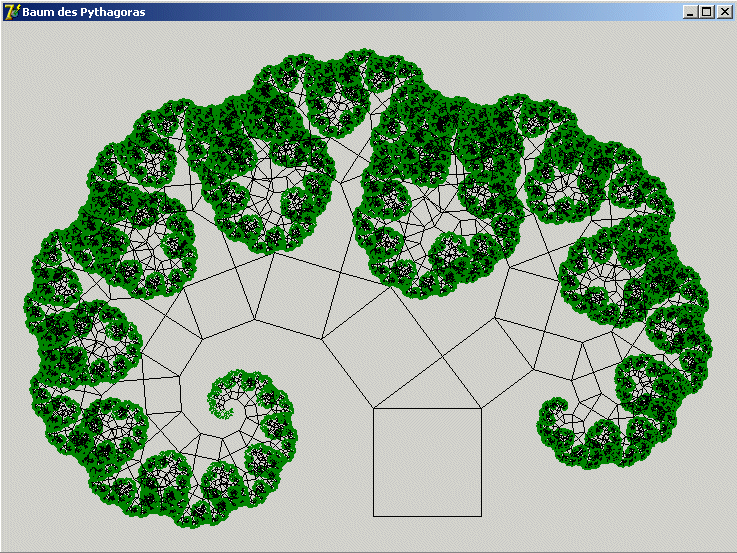
Der "Baum des Pythagoras" ist eine
selbstähnliche Figur. Folgendes Vorgehen ist
typisch für eine programmtechnische Behandlung solcher Figuren.
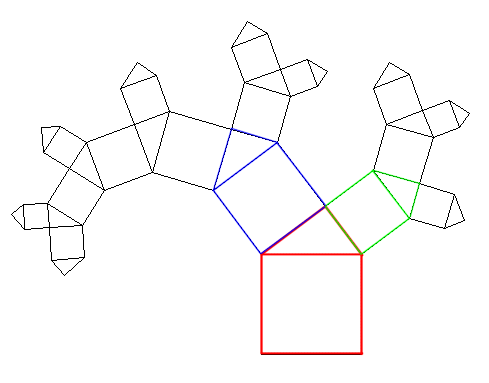
In der Skizze erkennt man, dass auf die Katheten der roten Figur eine - in der Größe passende
- blaue bzw. grüne Figur aufgesetzt wird. Das wiederholt sich entsprechend der Rekursionstiefe
bis schließlich die Katheten alleine gezeichnet werden. |
 |
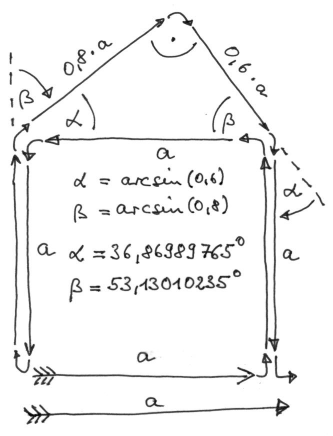 |
Bei der Konstruktion der Prozedur zeichneFigur(T,A) (T gibt die Rekursionstiefe an,
A die Größe der Figur) muss man beachten, dass die "einfache Figur" (hier eine Strecke) und die
"schwierige Figur" (hier Quadrat mit Dreieck) hinsichtlich Orientierung und Größe
zueinander passen müssen. Der nebenstehende Zeichenplan ist nicht optimiert und zeigt, dass
unter In-Kauf-Nahme von doppelt gezeichneten Strecken eine Lösung schnell gefunden werden kann. |
Lösung in Prolog
Das ist tatsächlich das komplette Programm!
zeichneFigur(0,A):-turtle_draw(A).
zeichneFigur(T,A):-turtle_draw(A),turtle_turn(90),turtle_draw(A),turtle_turn(90),
turtle_draw(A),turtle_turn(90),turtle_draw(A),turtle_turn(180),
turtle_draw(A),turtle_turn(-53.13010235),
T1 is T-1,A1 is 0.8*A,zeichneFigur(T1,A1),
turtle_turn(-90),
A2 is 0.6*A,zeichneFigur(T1,A2),
turtle_turn(-36.86989765),turtle_draw(A),turtle_turn(90).
baum:-turtle_init,turtle_moveto(100,420),zeichneFigur(12,100).

Lösung in Delphi
Der folgende Quelltext-Auszug zeigt den entscheidenden Kern. Natürlich ist außenherum ein
weiterer Aufwand zu treiben.
procedure TForm1.FormPaint(Sender: TObject);
procedure zeichneFigur(t : integer; a : real);
const
alpha = 36.86989765;
beta = 53.13010235;
tf = 5; // Rekursionstiefe für Farbwechsel
begin
if t < tf then canvas.Pen.Color := clGreen
else canvas.Pen.Color := clBlack;
if t = 0
then
TW.fd(a)
else
begin
TW.fd(a); TW.lt(90); TW.fd(a); TW.lt(90);
TW.fd(a); TW.lt(90); TW.fd(a);
TW.rt(180); TW.fd(a); TW.rt(beta);
if t > 0
then
zeichneFigur(t-1,0.8*a)
else
TW.fd(0.8*a);
TW.rt(90);
if t > 0
then
zeichneFigur(t-1,0.6*a)
else
TW.fd(0.6*a);
if t < tf then canvas.Pen.Color := clGreen
else canvas.Pen.Color := clBlack;
TW.rt(alpha);
TW.fd(a); TW.lt(90);
end;
end;
begin
TW.SetPos(0,-300);
zeichneFigur(20,150);
end;
baum_des_pythagoras.zip