HSG

Aktuelle Seite: HSG/Fächer/Informatik/Material/Prolog/Graphen

Tiefensuche (depth first search, dfs)

Tiefensuche versucht durch stetiges Erweitern eines Weges zum Ziel zu gelangen. Im Misserfolgsfall werden durch Backtracking andere Verzweigungen gewählt.

Algorithmus 1 zur Wegsuche von X nach Y mit Vermeidung von Zyklen (nach Informatik mit Prolog, Gerhard Röhner, S.61)
pfeil(a,b).
pfeil(a,c).
pfeil(a,d).
pfeil(b,c).
pfeil(c,d).
pfeil(c,e).
pfeil(d,e).
pfeil(c,a).

weg(X,Y):-pfeil(X,_),pfeil(_,Y),tiefensuche(X,Y,Loesung).

tiefensuche(Start,Ziel,Loesung):-tiefensuche(Start,[Start],Ziel,Loesung).

tiefensuche(Ziel,Pfad,Ziel,Loesung):-Loesung = Pfad,!.
tiefensuche(KnotenA,Pfad,Ziel,Loesung):-pfeil(KnotenA,KnotenN),
                                        not(member(KnotenN,Pfad)),
                                        tiefensuche(KnotenN,[KnotenN|Pfad],Ziel,Loesung).
In "tiefensuche(Ziel,Pfad,Ziel,Loesung):-Loesung = Pfad,!." wird ein Cut verwendet und es kommt die 'Akkumulatortechnik' zur Anwendung.

Tiefensuche kann im Einzelfall sehr ungünstig verlaufen.

Algorithmus 2 zur Wegsuche von X nach Y mit Vermeidung von Zyklen (nach Grundkurs Informatik, H.-U. Zimmermann, S.65)
  1. Zuerst wird geprüft, ob es Kanten von X weg und zu Y hin gibt. Nur so kann es einen Weg von X zu Y geben.
  2. Alle von X aus direkt erreichbaren Knoten werden in eine Nachfolger-Liste gespeichert.
  3. Die Weg-Liste wird mit [X] gestartet.
  4. Als Nachfolge-Knoten Z wird das erste Element der Nachfolger-Liste entnommen und der Weg-Liste hinzugefügt.
  5. Die Nachfolger-Liste wird vorne (Tiefensuche!) um mögliche Nachfolger ergänzt.
  6. In der Nachfolger-Liste werden schon besuchte Knoten gestrichen.
  7. Die Schritte 4 bis 6 werden solange wiederholt bis das Ziel Y erreicht ist oder die Nachfolger-Liste leer ist.
Umsetzung in Prolog
pfeil(a,b).
pfeil(a,c).
pfeil(a,d).
pfeil(b,c).
pfeil(c,d).
pfeil(c,e).
pfeil(d,e).

pfeil(c,a).

weg(X,Y):-pfeil(X,_),pfeil(_,Y),weg1(X,Y,[],[]).
weg1(Start,Ziel,Anwaerter,Besucht):-Start=Ziel,
                                    append(Besucht,[Ziel],Route),write(Route).
weg1(Start,Ziel,Anwaerter,Besucht):-append(Besucht,[Start],BesuchtNeu),
                                    findall(N,pfeil(Start,N),Nachfolger),
                                    append(Nachfolger,Anwaerter,AnwaerterNeu),
                                    subtract(AnwaerterNeu,BesuchtNeu,[K|R]),
                                    weg1(K,Ziel,[K|R],BesuchtNeu).
'Schachteldiagramm' zu weg1(a,e,[ ],[ ]).
Verwendete Systemprädikate:
append (append(L1,L2,L3) fügt die Listen L1 und L2 zu L3 zusammen),
findall ( findall(X,p(X),L) sammelt in der Liste L alle X, die p(X) wahr machen) ,
subtract ( subtract(A,B,D) ermittelt die Differenzmenge D = A\B )
Detail
Der Abbruch bei leerer Anwärterliste geschieht in subtract(AnwaerterNeu,BesuchtNeu,[K|R]) , weil [ ] = [K|R] fehlschlägt.

Vergleich der Algorithmen 1 und 2

Algorithmus 2 findet höchstens eine Lösung und ist aufwändiger, Algorithmus 1 findet alle Lösungen und ist kürzer.

Anwendung

In der Aufgabe 21 auf Seite 26 von G.Röhner, Informatik mit Prolog soll ein Weg von a nach g gesucht werden. Herr Röhner schlägt vor, das Labyrinth durch die vorhandenen Türen zu beschreiben. Da man eine Tür in beiden Richtungen beschreiten kann, lässt sich mit pfeil(X,Y):-tuer(X,Y). und pfeil(Y,X):-tuer(X,Y). eine Anpassung an obige Notation vornehmen. 
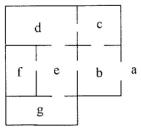
tuer(a,b).
tuer(b,e).
tuer(b,c).
tuer(d,e).
tuer(c,d).
tuer(e,f).
tuer(g,e).

pfeil(X,Y):-tuer(X,Y).
pfeil(X,Y):-tuer(Y,X).

tiefensuche(Start,Ziel,Loesung):-pfeil(Start,_),pfeil(_,Ziel),
                                 tiefensuche(Start,[Start],Ziel,Loesung).

tiefensuche(Ziel,Pfad,Ziel,Loesung):-Loesung = Pfad,!.
tiefensuche(KnotenA,Pfad,Ziel,Loesung):-pfeil(KnotenA,KnotenN),
                                        not(member(KnotenN,Pfad)),
                                        append(Pfad,[KnotenN],PfadNeu),
                                        tiefensuche(KnotenN,PfadNeu,Ziel,Loesung).
Obiges Programm verwendet eine leicht modifizierte Tiefensuche: Neue Knoten werden mit append hinten an den Pfad angehängt. So wird der Pfad am Schluss in der richtigen Orientierung ausgegeben. 
?- tiefensuche(a,g,L).

L = [a, b, e, g] ;

L = [a, b, c, d, e, g] ;