HSG

Aktuelle Seite: HSG/Fächer/Informatik/Material

Der Dreh-Algorithmus

Herleitung der Gleichungen für die Drehung um a um den Nullpunkt

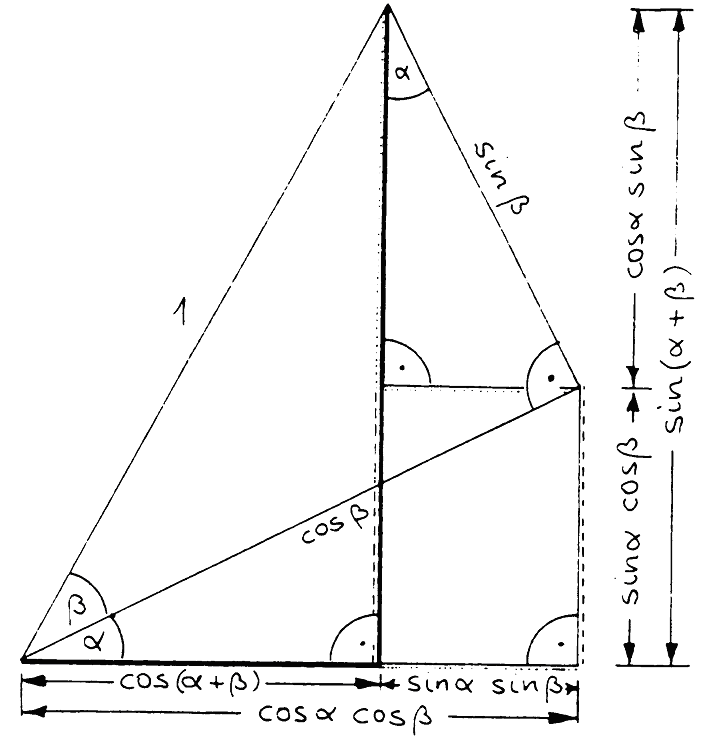
Voraussetzung sind die Additionstheoreme

(1) cos(α+β) = cos(α)*cos(β) - sin(α)*sin(β)
(2) sin(α+β) = cos(α)*sin(β) + sin(α)*cos(β)

und die Darstellung eines Punktes P(x/y) auf einem Kreis um den Nullpunkt mit Radius r:

(3) x = r*cos(β) und (4) y = r*sin(β), dabei ist β der Drehwinkel von der positiven x-Achse gezählt

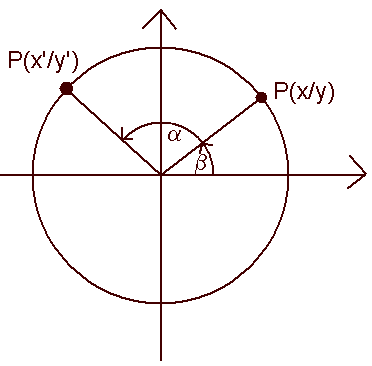Es gilt

(5) x' = r*cos(α+β) und
(6) y' = r*sin(α+β)

Mit den Additionstheoremen (1),(2) folgt

(7) x' = r*cos(α)*cos(β) - r*sin(α)*sin(β) und
(8) y' = r*cos(α)*sin(β) + r*sin(α)*cos(β)

Aus (7) und (8) folgen mit (3) und (4) die gesuchten Gleichungen:

x' = cos(α)*x - sin(α)*y
y' = sin(α)*x + cos(α)*y



Drehung um einen Punkt D(dx/dy):

Man verschiebt zuerst so, dass
der Punkt D(dx/dy) in den
Nullpunkt zu liegen kommt: 		Dann wird der Punkt gedreht: Und schließlich zurückgeschoben:
x' = x - dx
y' = y - dy
x'' = cos(α)*(x-dx) - sin(α)*(y-dy)
y'' = sin(α)*(x-dx) + cos(α)*(y-dy)
x''' = cos(α)*(x-dx) - sin(α)*(y-dy) + dx
y''' = sin(α)*(x-dx) + cos(α)*(y-dy) + dy


Eine mögliche Realisierung zeigt folgender Quelltext-Auszug:

  function gedreht(P,D : TPunkt; alpha : real) : TPunkt;
  begin
    result.X := cos(alpha)*(P.X-D.X) - sin(alpha)*(P.Y-D.Y) + D.X;
    result.Y := sin(alpha)*(P.X-D.X) + cos(alpha)*(P.Y-D.Y) + D.Y;
  end;


drehen.zip

Zur Herleitung der Summenformeln: