|
|||
| HSG |
|
Modellierung einer Turtle-Grafik
....Klassendiagramm und Zuständigkeiten
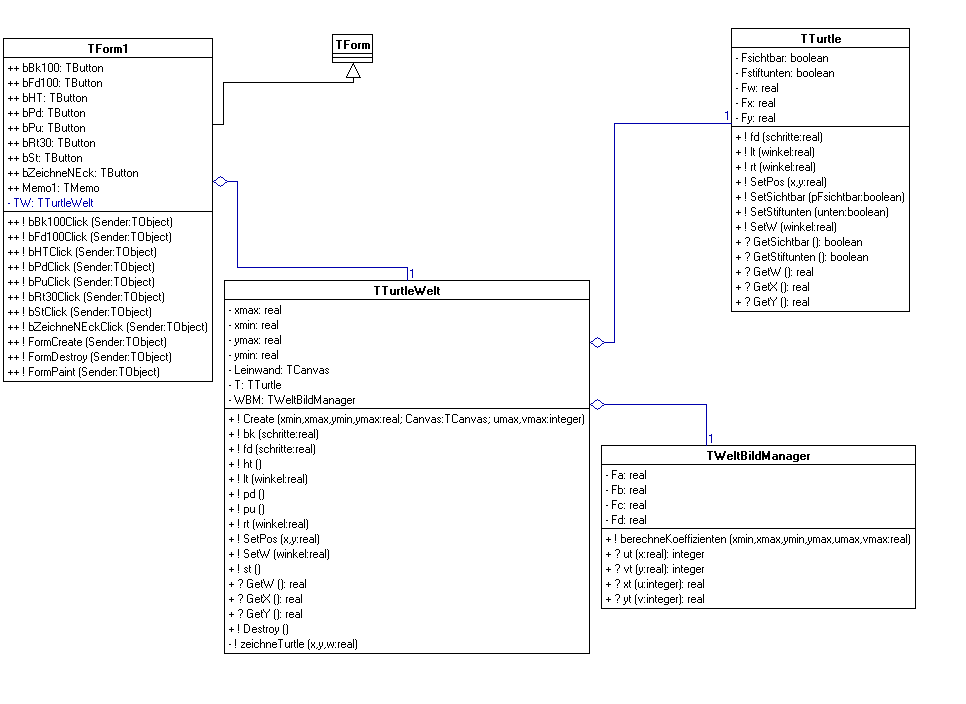
Das Formular "Form1" ist wie häufig das "Mutterobjekt", das hier das TurtleWelt-Objekt "TW" hat. Es ist also für die Erzeugung und Vernichtung der TurtleWelt zuständig. In obigem Diagramm sind übrigens viele Test-Befehle und -Buttons berücksichtigt, die eigentlich nur mit der Verwendung der Turtle zu tun haben.
Die TurtleWelt hingegen ist für die Abmessungen der Welt, für die Turtle selbst und für das Zeichnen zuständig. Wenn man der Turtle Befehle gibt, so gibt man sie eigentlich der TurtleWelt, die sie einerseits an die Turtle weiterleitet, als auch eventuelles Zeichnen veranlasst. TurtleWelt lässt sich die notwendigen Transformationen von einem Welt-Bild-Manager erledigen, der als "Software-IC" erprobt und dokumentiert vorliegt. Notwendige Informationen über Abmessungen der "Welt" oder über die Leinwand, auf der gezeichnet werden soll, werden der TurtleWelt gleich beim Erzeugen durch einen modifizierten Konstruktor übergeben. Dieser Kontruktor übernimmt auch die Erzeugung des Welt-Bild-Managers und der Turtle.
Die Turtle selbst hat in dieser Modellierung nichts mit dem Zeichnen zu tun und verwaltet eigentlich nur Ort und Orientierung, sowie Stift- und Sichtbarkeitszustände. Aus Gründen der Genauigkeit werden Ort und Winkel als real-Zahlen gespeichert. Die "virtuelle" Turtle kann also auch 3,234 Schritte exakt tun und sich um 47,35° exakt drehen. Was man sieht, ist nur der "View" der Turtle, der natürlich auf volle Pixel gerundet dargestellt wird.
...
Entwurf einer Prozedur arc, die der Turtle Bogenzeichnen beibringt
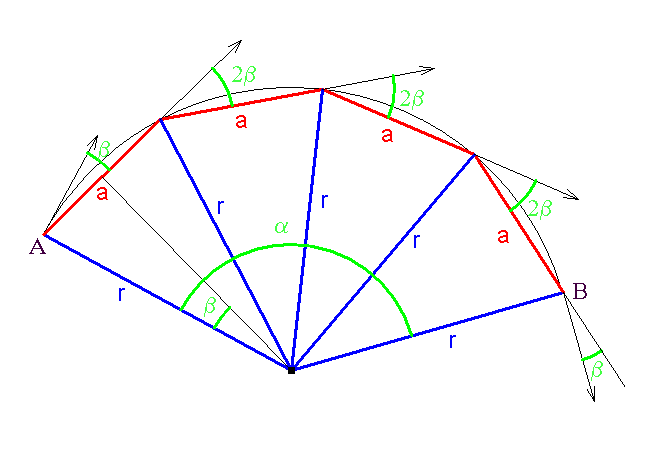
Das Bogenstück von A nach B soll von der Turtle gezeichnet werden. Dabei soll die Blickrichtung der Turtle am Anfang und am Ende des Bogens tangential sein. Das Bogenstück wird durch den Radius r, den Winkel α und die Drehrichtung charakterisiert. Das Bogenstück soll durch einen Polygonzug angenähert werden, in obiger Skizze mit n = 4 Teilstücken der Länge a.
Man entnimmt der Skizze die Beziehungen
| β := α/(2*n); | sin(β) = (a/2)/r ⇒ a := 2*r*sin(β); |
Einfache Winkelüberlegungen zeigen, dass die Turtle sich am Anfang und Schluss um β, zwischendurch um 2*β drehen muss. Bei der Programmierung wurde n aus der Anzahl der vollen Grad-Schritte ermittelt. Die Option, dass die Eingabe eines negativen Winkels ein Rückwärtsdrehen bewirken soll, führt zu einigen Fallunterscheidungen. Außerdem muss nartürlich das Bogenmaß verwendet werden.
procedure TTurtleWelt.arc(r,alpha : real; d : shortint);
var
n,i : integer;
w,a : real;
begin
n := round(abs(alpha));
w := abs(alpha)/(2*n); a := 2*r* sin(w/180*pi);
if d*alpha > 0 then rt(w) else lt(w);
for i := 1 to n-1 do
begin
if alpha > 0 then fd(a) else bk(a);
if d*alpha > 0 then rt(2*w) else lt(2*w);
end;
if alpha > 0 then fd(a) else bk(a);
if d*alpha > 0 then rt(w) else lt(w);
end;
|
turtle0.zip