 |
|||
| HSG |
|
Subtraktionskatastrophe, Auslöschung
Es sollen die Verhältnisse durch "Modell-Fließkommazahlen" veranschaulicht werden. Diese Zahlen haben z.B. folgendes Format:
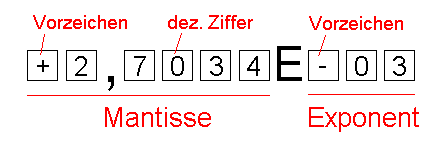
Der Einfachheit halber darf man für die Vorzeichen '+,-' und für die Ziffern '0,1,..,9' verwenden.
In dieser Darstellung gilt 1/2 = +5,0000E-01 und 35/71 = +4,9296E-01. Rechnet man jetzt 1/2-35/71 so erhält man zunächst +5,0000E-01 - +4,9296E-01 = +0,0704E-01 = +7,0400E-03. Die beiden roten Nullen sind dabei nur durch die Normalisierung 'hereingerutscht', sie haben keinen Informationsgehalt. Mit dem Taschenrechner errechnet man 1/2-35/71 = 0,007042253 = 7,042253E-3, dh. die 'beste Approximation' als Modell-Fließkommazahl wäre 7,0423E-03. Die Ziffern 2 und 3 wurden durch die begrenzte Stellenzahl der Mantisse und durch die etwa gleich großen Minuend und Subtrahend 'ausgelöscht'.
Folgerung
Beim Rechnen mit Fließkommazahlen ist eine Differenz von etwa gleich großen Zahlen zu vermeiden!
Beispiel
Bei der π-Bestimmung nach Archimedes tritt ursprünglich die Zuweisung
s := sqrt(2-sqrt(4-s*s));
auf. Hier nähert sich die innere Wurzel immer mehr dem Wert 2, sodass eine 'Subtraktionskatastrophe' eintritt. Ein geschicktes Erweitern

ergibt die Zuweisung
s := s/sqrt(2+sqrt(4-s*s));
, die die Auslöschung vermeidet. Sofort erhält man um Klassen bessere numerische Ergebnisse.