Folgender Algorithmus in Pascal-Notation (D.Herrmann, Algorithmen Arbeitsbuch, S. 31) liefert die Potenz a^b für reelles a>0 und natürliche Zahlen b:

x := a; y := b; z := 1;
while y > 0 do
begin
  if odd(y) then z := z*x;
  y := y div 2;
  x := x*x;
end;

Aufgaben

• Implementiere und teste den Algorithmus.
• Finde Vorbedingung, Schleifeninvariante (Vorschlag {z*x^y = a^b}) und Nachbedingung und führe einen formalen Korrektheitsbeweis.
• Zeichne ein Struktogramm mit Zusicherungen.
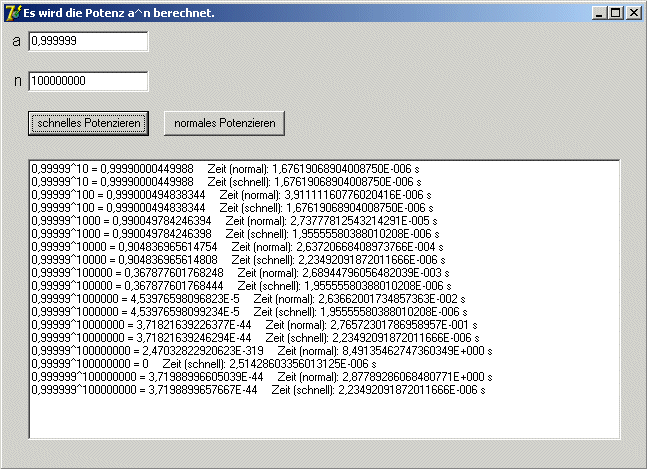
• Implementiere den 'naiven' Potenzierungsalgorithmus (for-Schleife) und vergleiche die beiden Algorithmen durch Zeitmessungen ( Delphi, Python). Dokumentiere deine Tests.

Lösung in Delphi

potenz.zip