Von der Quadratur des Rechtecks zum Pythagoras

Von der "Quadratur des Rechtecks" zum Pythagoras mk, Mai 99
Es wäre günstig, wenn vor der Reihe z.B. im Rahmen der täglichen Übungen der Flächeninhalt eines Parallelogramms und der Satz von Thales wiederholt wurden.

1. Stunde, "Verwandlung eines Rechtecks in ein flächengleiches mit vorgegebener Seite"

Hinführende Hausaufgabe:
Zeichne das Parallelogramm ABCD mit A(0/0), B(8/0), C(11/5) und D(3/5). Berechne dann den Flächeninhalt auf zwei Arten.

Gemeinsam wird nun folgende Skizze erarbeitet, bei der durch entsprechende farbliche Hervorhebungen der Augenmerk vom Parallelogramm auf die beiden - flächengleiche - Rechtecke gelenkt wird.

mk9_1.geo
Dieses und die weiteren Bilder sind Ausschnitte aus Euklid -Programmen, die zur eigenen Verwendung geladen werden können.

Warum Quadratur ?
Problem:
Wie vergleicht man Flächeninhalte ohne zu rechnen?
Ist das rote oder das grüne Rechteck größer?

Aufgabe (in Gruppenarbeit):
Aus einem - grünen - Rechteck der Breite 7 cm und der Höhe 3 cm soll eines neues - rotes - Rechteck mit der Höhe 5 cm entstehen.
Impulse:
Wo sollten in der Skizze die Längen 7cm und 3 cm eingetragen werden? Wo sollte die Länge 5cm eingetragen werden?

mögliche Lösung :

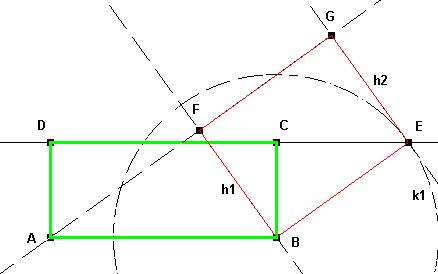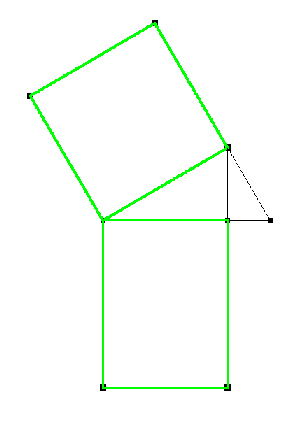
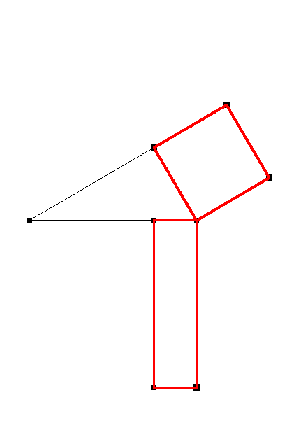
Konstruktionsbeschreibung:

1. Gerade (CD)
2. Kreis k1 um B mit r = 5 cm schneidet (CD) in E
3. Strecke BE
4. Parallele g zu (BE) durch A
5. Orthogonale h₁ zu (BE) in B schneidet g in F
6. Orthogonale h₂ zu (BE) in E schneidet g in G
7. BEGF ist das gesuchte flächengleiche Rechteck

Hausaufgabe:
1. Zeichne das Parallelogramm ABCD mit A(0/0), B(10/0), C(16/2) und D(6/2). Berechne dann den Flächeninhalt auf zwei Arten.
2. Verwandle das Parallelogramm in ein flächengleiches Rechteck mit a = 3 cm (4 cm, 5 cm, 6cm).

2. Stunde, "Die Quadratur des Rechtecks"

Hausaufgabenbesprechung

Die (Fast-) Quadratur durch Probieren
Ein auf einem Arbeitsblatt (DIN A4 quer, links etwa 3 cm hoch, 13 cm breit) vorgegebenes Rechteck wird in ein anderes Rechteck verwandelt. Dies geschieht in arbeitsteiliger Partnerarbeit, wobei die vorgegebene Höhe von etwa 3,5 cm bis etwa 12 cm varriiert wird. Das erhaltene Rechteck soll farblich hervorgehoben werden. Gemeinsam werden die Blätter der Gruppen "geordnet" an die Wand gehängt. Es entsteht ein "Film" etwa der folgenden Art.

Im Unterrichtsgespräch wird erarbeitet, dass es unter den konstruierten Rechtecken fast, unter den konstruierbaren Rechtecken sicher ein Quadrat gibt.
Bemerkung: Im Euklidprogramm pyth20.geo läßt sich dieses Quadrat durch "Ziehen" eines Punktes ermitteln.

Finden der Konstruktion zur Quadratur
In Gruppen (4-5er Gruppen, Gruppenbildung wie bei letzter GA) soll nun die exakte Konstruktion gefunden werden. Grundlage ist ein Arbeitsblatt auf dem für zwei verschiedene Rechtecke die Quadratur durch Probieren durchgeführt wurde. Zur Sicherung wird die Konstruktion gemeinsam einschließlich der Konstruktionsbeschreibung an der Tafel / im Heft durchgeführt.

Quadratur des Rechtecks

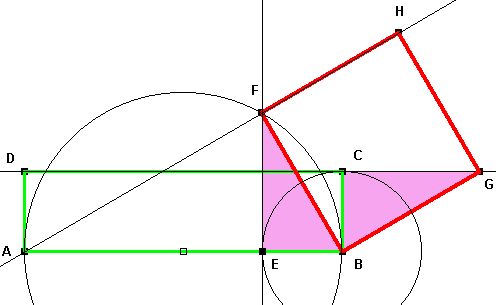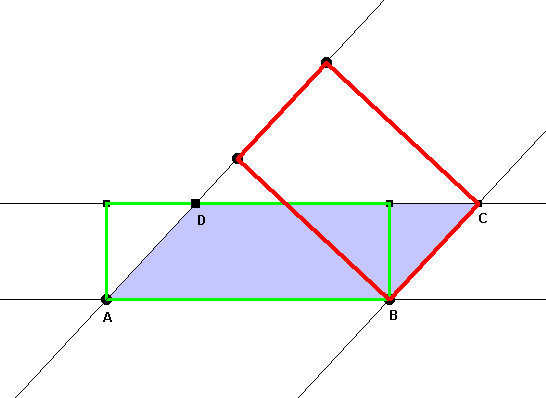
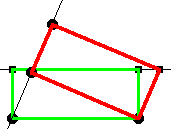
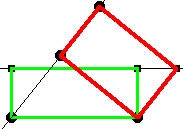
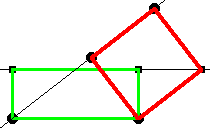
Konstruktionsbeschreibung:

1. Thaleskreis über AB
2. E auf AB mit Länge von EB = Länge von BC
3. Lot auf AB in E
4. Lot schneidet Thaleskreis in F
5. Gerade (AF)
6. Parallele zu (AF) durch B schneidet (DC) in G
7. H ergänzt FBG zum Quadrat

Warum ist FBGH ein Quadrat?
Die rechten Winkel und die Parallelität gegenüberliegender Seiten ergeben sich aus der Konstruktion.
Die Dreiecke DEBF und DBGC sind nach dem WSW-Satz (90°-Winkel, Länge EB = Länge BC, Winkel bei B) kongruent. Insbesondere sind also die Seiten BF und BG gleich lang.

Hausaufgabe:
Konstruiere zu Rechtecken mit a₁=8cm, b₁=3cm und a₂=7cm, b₁=5cm jeweils ein flächengleiches Quadrat.

3. Stunde, "Der Satz des Pythagoras"

Hausaufgabenbesprechung

Eine Variante der Quadraturkonstruktion

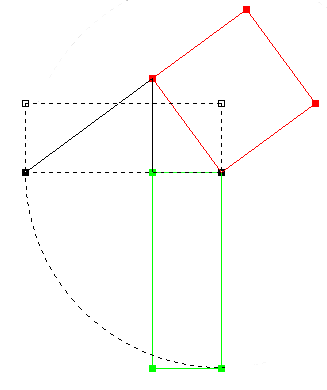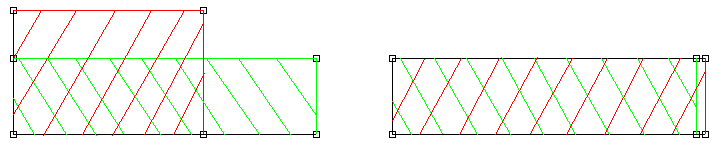
Der Lehrer zeigt eine Variante der Konstruktion mit einem um 90° gedrehten Rechteck.
Es ist ein Vorteil dieser Konstruktion, dass das Rechteck und das Quadrat nicht übereinander liegen.

Gemeinsam wird nun im Unterrichtsgespräch an der Tafel / im Heft das Rechteck mit b₁=2cm, h₁=7cm nach dieser Konstruktion in ein flächengleiches Quadrat verwandelt. Parallel zur Konstruktion kann eine Konstruktionsbeschreibung notiert werden.
Zur Übung soll anschließend in Einzel-bzw. Partnerarbeit eine analoge Konstruktion für ein Rechteck mit b₂=5cm, h₂=7cm durchgeführt werden. Allerdings soll nun das entstehende Quadrat links, dh. gewissermaßen spiegelbildlich liegen.

Was fällt bei den letzten beiden Figuren auf?

Gilt für zwei Rechtecke mit der Höhe a und den Breiten b₁ und b₂
b₁+ b₂=a, so entstehen bei den Quadraturen zwei kongruente rechtwinklige Dreiecke.

Die Höhe des rechtwinkligen Dreieck liegt einmal b₁ von rechts und einmal b₂ von links auf der Grundseite entfernt.

Zwei Quadraturen ergeben 3 Quadrate
Um sicherzustellen, dass alle die Konstruktionen im Heft haben und um für die Hausaufgabe etwas zum Ausschneiden zu haben, wird ein Arbeitsblatt mit folgendem Inhalt ausgeteilt:

Bereitet man die beiden Figuren auch auf getrennten Folien (obiges Arbeitsblatt zerschnitten) vor, so werden die Schülerinnen und Schüler die Pythagorasfigur durch Übereinanderlegen herstellen.

Hausaufgabe:
1. Überschrift "Satz des Pythagoras"
2. Schneide beide "Quadraturfiguren" aus dem Arbeitsblatt aus und klebe sie so (etwa nur an den äußeren Teilen der Quadrate Klebstoff) ein, dass man weiterhin sowohl das eine oder das andere rechtwinklige Dreieck nach oben legen kann.
3. Konstruiere eine Pythagorasfigur (Maße des rechtwinkligen Dreiecks: a=6cm, b=8cm, c=10cm) und färbe flächengleiche Quadrate und Rechtecke gleich ein.

interaktives Euklid-Arbeitsblatt

Bemerkung:
Der Kathetensatz (Satz von Euklid) ist durch die Quadratur bereits bewiesen. Der Satz des Pythagoras braucht durch die anschaulich offensichtliche Ergänzung der beiden Figuren nicht mehr bewiesen werden. Es fehlt der Höhensatz. Der kann wie die genannten Sätze auch, in einer späteren Stunde aufgrund der Verhältnisse in ähnlichen Dreiecken in der Pythagorasfigur bewiesen werden. Das ist eine gute Anwendung bzw. Wiederholung der Ähnlichkeit.

05.06.99 Klaus Merkert

zurück zur HSG-Mathematikseite