 |
|||
| HSG |
|
Problem
Bei der Übertragung von Nachrichten passieren bei höheren Baudraten, langen
Kabellängen, Timing-Problemen oder warum auch immer mehr oder weniger Fehler.
Der menschliche Empfänger kann bei einem Text aus dem Zusammenhang oft
leicht erkennen, dass die Übertragung gestört wurde. Aber was ist, wenn z.B.
eine Binär-Datei (z.B. *.exe) übertragen wird? Hier ist aus der Bitfolge nur
schwer bis garnicht erkennbar, ob sie verändert wurde. Wir hätten aber gerne,
dass auch ein 'seelenloser' Computer Fehler entdecken kann.
Aufgabe
Das Bild zeigt in den ersten beiden Zeilen zwei Bitmuster nach dem miniRS232-Protokoll. Welche Zeichen wurden gesendet? Die letzten beiden Zeilen entstanden durch eine Überlagerung der beiden Bitmuster. Welchen Alltagsvergleich findet man zu einer Überlagerung? Eine der Überlagerungen kann man schnell als fehlerhaft erkennen, warum? Der anderen Überlagerung sieht man das gar nicht an. Welches Zeichen könnte so gesendet worden sein?
Lösungsmöglichkeiten
1. Paritätsbit
Das Paritätsbit dient der Erkennung von Fehlern in einer Folge von übertragenen Bits. Es gibt gerade (even, E) und ungerade (odd, O) Parität. Das Prüfbit wird nun so ermittelt: Es werden die Einsen in der Bitfolge gezählt und das Zusatzbit so gewählt, dass sich insgesamt eine gerade bzw. ungerade Anzahl von Einsen ergibt.
Beispiele für ungerade Parität:
0100 1110 hat vier Einsen, damit die Gesamtzahl ungerade wird, wird eine
Eins ergänzt.
Es wird also die Nachricht 0100 1110 1
gesendet.
1011 0110 hat fünf Einsen, da die Anzahl schon ungerade ist, wird eine
Null ergänzt.
Es wird also die Nachricht 1011 0110 0
gesendet.
2. Prüfsumme
Beispiel:
3-byte-Nachricht: 7,24,11 Prüfsumme: 7+24+11 = 42 übertragen: 7,24,11,42
Empfänger rechnet und vergleicht: 7+24+11 = 42, 42 = 42, alles in Ordnung!
Fehlerfälle:
7+23+11 = 41 ≠ 42, Fehler erkannt!
6+24+12 = 42 = 42, Fehler nicht erkannt!
24+7+11 = 42 = 42, Fehler nicht erkannt!
3. "Prüfreste"
Das Prüfsummen-Verfahren war leicht auszuhebeln, vielleicht ist ein "Prüfquotienten-Verfahren" besser:
Nachricht: 7,24,11 aus den Bytes wird eine 9-stellige Zahl gebildet: 007024011, die Zahl wird durch einen festen "geeigneten" Divisor geteilt: 007024011 : 171 = 41 076 Rest 15, der Rest wird als "Prüfzahl" benutzt
übertragen: 7,24,11,15
Fehlerfälle:
7,23,11 -> 41 ≠ 15, Fehler erkannt!
6,24,12 -> 24 ≠ 15, Fehler erkannt!
24,7,11 -> 150 ≠ 15, Fehler erkannt!
>>> 7024011%171 15 >>> 7023011%171 41 >>> 6024012%171 24 >>> 24007011%171 150
4. Cyclic Redundancy Code - CRC
Tatsächlich hat sich die Grundidee vom "Prüfrest" als sehr geeignet erwiesen, allerdings in mathematisch deutlich verfeinerter Form.
Beispiel
Aus der Nachricht wird ein Polynom mit den Koeffizienten 0 und 1 erzeugt:
1001 1011 --> 1*x7+0 *x6+0*x5+1*x4+ 1*x3+ 0*x2+1*x1+ 1*x0
Dieses Polynom wird durch ein Generator-Polynom z.B. x4+x+1 geteilt.
Das Rest-Polynom liefert über seine Koeffizienten den "CRC-Wert".
Die Arithmetik ist hier eigentümlich, es gibt z.B. keine Überträge, Addition und Subtraktion sind gleich. (0 + 1 = 1, 0 - 1 = 1, 1 + 1 = 0, ...)
Beispiel 1
Nachricht: 1001 1011, Generator-Polynom: 10011 (Grad 4) Division: 100110110000 : 10011 = 10000011 10011 ----- 00 00 -- 01 00 -- 11 00 -- 110 000 --- 1100 0000 ---- 11000 10011 ----- 010110 10011 ----- 00101 Rest = 4-Bit-CRC-Wert (die erste - fünfte von rechts - Ziffer ist immer 0)
Probe:
10000011 = x7+x+1, 10011 = x4+x+1
(x7+x+1)·(x4+x+1) = x11+x5+x4+x8+x2+x+x7+x+1 = x11+x8+x7+x5+x4+x2+1 = 100110110101
Bitte bedenken: x+x = (1+1)·x = 0x = 0 100110110101 + 0101 ------------ 100110110000
Beispiel 2
Nachricht: 10011011, Generator-Polynom: 101 (Grad 2) Division: 1001101100 : 101 = 10110110 101 --- 00111 101 --- 0100 101 --- 00111 101 --- 0100 101 --- 0010 000 --- 010
Es kommt seltsam vor, dass 101 in 100 passt, aber wenn man 100 - 101 rechnet bleibt sogar der Rest 001. Faustregel: Es kommt nur auf das höchste Bit an, ob der Divisor reinpasst.
Beispiel 3
In dem Buch von Tanenbaum, Computernetzwerke, 4.Auflage findet man auf Seite 487 das Beispiel:
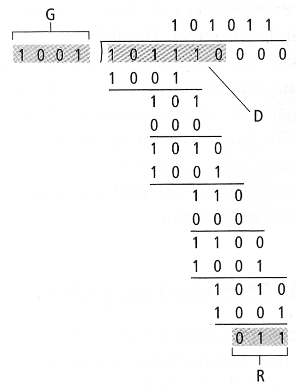
CRC-Prüfsummen lassen sich mit einfachen Schieberegisterschaltungen hardwaremäßig - also schnell - berechnen. Die Wahl des Generator-Polynoms ist für die Qualität des Verfahrens entscheidend. Manche Polynome wie CRC-16 oder auch CRC-4 sind genormt.
CRC-Demo-Programm
Delphi-Projekt: crc0.zip, *.exe: crc0_exe.zip
Aufgabe
Wähle eine 16-Bit-Nachricht N, z.B. N = 1001 1101 0001 1101. Teste, ob mit dem Polynom 10011 alle 1-Bit-Fehler gefunden werden. Bündelfehler ( Fehler, die voneinander abhängig sind) treten bei der Nachrichtenübertragung häufig auf z.B. durch Funken, Übersprechen. Hier wird ein Bündel aufeinanderfolgender Bits gestört (Was nicht heißt, dass die Bits genau herumgedreht sind.). Untersuche, ob Bündelfehler entdeckt werden.
Quelltext-Auszug aus dem Delphi-Programm
// nachricht und polynom sind als Zeichenketten aus '0' und '1' dargestellt
lp := Length(polynom); n := Length(nachricht);
for j := 1 to lp-1 do nachricht := nachricht+'0';
schieberegister := copy(nachricht,1,lp);
for i := 1 to n do
begin
if schieberegister[1] = '1'
then
for j := 1 to lp do
if schieberegister[j] = polynom[j]
then
schieberegister[j] := '0'
else
schieberegister[j] := '1';
if i < n then
schieberegister := copy(schieberegister,2,lp-1)+nachricht[lp+i];
end;
Eine entsprechende Python-Funktion
Mit debug == True wird ein Ausdruck 'wie von Hand gerechnet' erreicht.
debug = True
def crc(nachricht,polynom = '10011'):
"""
zu der 'nachricht' und zu dem 'polynom' (Strings aus 0 und 1)
wird die CRC-'Prüfsumme' berechnet (String aus 0 und 1)
"""
lp = len(polynom)
ln = len(nachricht)
# an die Nachricht so viele Nullen anhängen wie der Grad des Generatorpolynoms beträgt
for j in range(lp-1):
nachricht = nachricht+'0'
if debug:
print(nachricht)
if nachricht[0] == '0':
print('0'*lp)
else:
print(polynom)
print('-'*lp)
nachricht = list(nachricht)
schieberegister = nachricht[:lp]
for i in range(ln):
if schieberegister[0] == '1':
for j in range(lp):
if schieberegister[j] == polynom[j]:
schieberegister[j] = '0'
else:
schieberegister[j] = '1'
if i < ln-1:
schieberegister = schieberegister[1:lp]+list(nachricht[lp+i])
if debug:
print(' '*(i+1)+''.join(schieberegister))
if schieberegister[0] == '1':
print(' '*(i+1)+polynom)
else:
print(' '*(i+1)+'0'*lp)
print(' '*(i+1)+'-'*lp)
if debug and (i == ln-1):
print(' '*i+''.join(schieberegister))
return ''.join(schieberegister[1:])
CRC mit Hardware
Eine nähere Erläuterung findet man auf der Seite der FH Flensburg. Im vorliegenden Fall wurde crc('10101010') == '1001' berechnet. Bitte beachten, dass das untere Schieberegister und das Polynom von rechts nach links zu lesen ist. Zum Starten muss man zunächst einen Reset auslösen und dann die Eingabewerte einlesen. Nach dem Umstellen auf Schiebebetrieb sind 12 Takte notwendig. Der Zähler ist hier nur zum bequemen Mitzählen in der Schaltung. Er kann aber auch dazu dienen, den ganzen Vorgang zu automatisieren.
Die Schaltung crc1.hds wird durch das festverdrahtete Polynom '10011' wesentlich einfacher und schneller.
Links
- Paritätsbit bei wikipedia
- Paritätskontrolle des Mönches Werimbold aus 'Von Zahlen und Größen' von Heinz Lüneburg
- Prüfsumme bei wikipedia
- CRC bei wikipedia
- CRC - www.inf.fh-flensburg.de/lang
- CRC-Verfahren - auch mit Hardware
- Fehlerbehandlung - Vorlesungsmitschrift von Christiane Müller