 |
|||
| HSG |
|
Definition
Polyalphabetische Ersetzungschiffren bezeichnen in der Kryptographie Formen der Textverschlüsselung, bei der einem Buchstaben/Zeichen jeweils ein anderer Buchstabe/Zeichen zugeordnet wird. Im Gegensatz zur monoalphabetischen Substitution werden für die Zeichen des Klartextes mehrere Geheimtextalphabete verwendet.
aus wikipedia
Vigenère-Verschlüsselung
Das Dokument vigenere.pdf enthält ein Vigenère -Schema und ein Beispiel.
Aufgabe 1
Entschlüssele den nach Vigenère mit dem Schlüssel CAESAR verschlüsselten Geheimtext 'FIIOUVTFIDSZPDKWFRNLIF'.
Aufgabe 2
Entschlüssele folgenden nach Vigenère verschlüsselten Geheimtext (aus Beutelspacher, Kryptologie, S.42, Aufgabe 7) OHNE Schlüssel mit Hilfe von CrypTool (Analyse/Algorithmen/Vigenère).
PYIPJMHQYWECJMZQXZZDAGRDT XUZCWPYMSYQHVBWIUICWOBJEF PTNKFLCXKDEYIGSQBIOFPYZXW DTNOAVUVRJUAVXEUMJSGZCEBG YULPVUYJMZDCWDWZUCLWDNZCK FCVCKMHWKFSMYKLFYVBSGZXBM ZXJOAZYINABFFWSFCJMZQHKKW FCXUWUNEEJBLRULUMTRWECEDW DYJCWMHUOJWLPZLAAIKHTCVNS ZHCWSXNVBNAHEOMZOENVDYZCK UAAKZDYELWEWYVGEMMSYQHVBW PUJCWDHLXYQHLOYQHUFWDGFOY QHVBOALSOFTUSOMZXJOAZFVLW ZELOFRNZQVQLNSKEYECUTUWDO UXDOFIICVW
Der Kasiski-Test
nach Simon Singh, Geheime Botschaften, S.92 :
Klartext: DIELILIEDIEROSEUNDDIETULPE Schlüsselwort: GELBGELBGELBGELBGELBGELBGE Geheimtext: JMPMOPTFJMPSUWPVTHOJKXFMVI
Wie kommt es, dass das Wort 'DIE' beim ersten und zweiten Mal mit 'JMP' und beim dritten Mal mit 'OJK' verschlüsselt wurde?
Was weiß man über den 1., den 5., den 9. den 13., .... Buchstaben des mit dem Schlüssel GELB verschlüsselten Geheimtexts?
Historisch wurde die Kryptoanalyse von Kasiski zur Vigenère-Verschlüsselung schon vorher von Babbage gefunden, der sie aber nicht veröffentlichte.
kleines Delphi-Programm dazu: kasiski.zip
Autokorrelation
Der Autokorrelationstest geht wie der Kasiski-Text davon aus, dass einerseits im Klartext immer wieder bestimmte Silben vorkommen, andererseits diese Silben ab und zu durch die gleichen Buchstaben des Schlüsselwortes verschlüsselt werden. Das lässt vermuten, dass die Wahrscheinlichkeit für Übereinstimmungen zwischen Geheimtext und verschobenem Geheimtext bei einer Verschiebung um ein Vielfaches der Schlüssellänge am größten sein müsste. Wir wollen das an einem angeblich Vigenère-verschlüsselten Text vig0.txt prüfen, der als Entschlüsselungsaufgabe im Internet gefunden wurde. Zur Demonstration und zur Entschlüsselung wird wieder ein kleiner 'funktionaler Werkzeugkoffer' vigenere0.pyverwendet.
def autokorr(t,n):
"""
ermittelt die Anzahl der Uebereinstimmungen des um n verschobenen Textes t,
'herausgeschobene' Teile werden vorne angesetzt
"""
m = len(t)
return len([t[i] for i in range(m) if t[i] == t[(i+n)%m]])
Zuerst sollen Experimente zur Autokorrelation gemacht werden. Der geheime Text liegt im String t vor.
>>> for i in range(30): print(i,autokorr(t,i)) 0 1000 1 24 2 52 3 35 4 80 5 34 6 32 7 31 8 101 9 29 10 49 11 41 12 66 13 38 14 41 15 41 16 89 17 44 18 52 19 48 20 84 21 29 22 39 23 28 24 66 25 31 26 49 27 32 28 90 29 43
1000 Übereinstimmungen bei Verschiebung 0 bedeuten natürlich, dass t aus 1000 Zeichen besteht. Wahrscheinlich sieht man trotz aller Unregelmäßigkeit eine gewisse Periodizität. Die Zahlen sind schnell in eine Tabellenkalkulation (autokorr.ods kopiert und lassen sich grafisch darstellen.
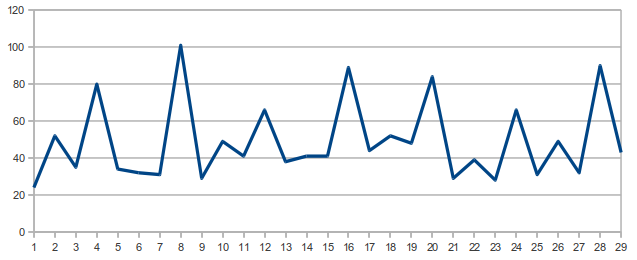
Die 'Spitzen' scheinen im Abstand von 4 aufzutreten. Das deutet auf eine Schlüssellänge von 4 hin. Die Funktion keylen versucht die Ermittlung der Schlüssellänge zu algorithmisieren. Die Funktion ist experimentell und kann sicher verbessert werden.
import math
def keylen(t):
"""
macht bei einem Vigenere-verschluesselten Text über Autokorrelation
einen Vorschlag über die Schluessellaenge
"""
n = len(t)
dak = sum([autokorr(t,i) for i in range(n)])/n # durchschnittliche AK
sab = math.sqrt(sum([(autokorr(t,i)-dak)**2 for i in range(n)])/n)
spitzen = [i for i in range(n) if autokorr(t,i) > dak+0.1*sab]
lens = len(spitzen)
diff = qsort([spitzen[i+1]-spitzen[i] for i in range(lens-1)])
print(diff) # DEBUG
return diff[int(3*len(diff)/4)]
Eine probeweise Anwendung auf obigen Geheimtext aus dem Beutelsbacher-Buch ergab jedenfalls die - richtige - Schlüssellänge 5. Bei t liefert die Funktion wie erwartet 4.
>>> keylen(g) [1, 1, 1, 1, 2, 2, 3, 3, 3, 3, 3, 3, 4, 4, 4, 4, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 7, 7, 7, 7, 10, 10, 10] 5
Weiß man, dass die Schlüssellänge 4 beträgt, so ist der Geheimtext in 4 'Spalten' aufzuteilen, die ja jeweils monoalphabetisch Caesar-verschlüsselt sind.
>>> s = aufteilen(t,4)
>>> frequency(s[0])[:5]
[('M', 0.188), ('V', 0.124), ('Q', 0.096), ('A', 0.068), ('Z', 0.064)]
In der ersten 'Spalte' kommt 'M' mit 18,8% vor. Vermutlich hängt das daran, dass der Geheimbuchstabe 'M' aus dem Klartextbuchstaben 'E' entstanden ist. Jetzt kann der Schlüsselwortbuchstabe, der die Verschiebung von 'E' zu 'M' bewirkt, ermittelt werden.
def schluessel(k,c):
"""
ermittelt den Buchstaben v, sodass der Klartextbuchstabe k
mit einer Verschiebung gemäß v auf den Geheimbuchstaben c
zu liegen kommt
"""
An = ord('A')
kn = ord(k)-An
cn = ord(c)-An
return chr((cn-kn)%26+An)
Shell:
>>> schluessel('E','M')
'I'
>>> schluessel('E','V')
'R'
Der erste Buchstabe des Schlüsselwortes ist also ein 'I', oder auch ein 'R'. Der zweite Buchstabe wird analog eingekreist:
>>> frequency(s[1])[:5]
[('A', 0.12), ('N', 0.12), ('R', 0.12), ('V', 0.12), ('E', 0.076)]
>>> schluessel('E','A')
'W'
>>> schluessel('E','N')
'J'
>>> schluessel('E','R')
'N'
>>> schluessel('E','V')
'R'
Leider gibt es gleich vier Kandidaten: W, J, N, oder R.
>>> frequency(s[2])[:5]
[('H', 0.132), ('Q', 0.132), ('D', 0.088), ('U', 0.08), ('K', 0.076)]
>>> schluessel('E','H')
'D'
>>> schluessel('E','Q')
'M'
Der dritte Buchstabe ist vermutlich D oder M.
>>> frequency(s[3])[:5]
[('A', 0.208), ('J', 0.108), ('N', 0.084), ('E', 0.08), ('D', 0.08)]
>>> schluessel('E','A')
'W'
Der vierte Buchstabe ist vermutlich ein 'W'.
Nach etwas Probieren am zweiten Buchstaben ergibt sich:
>>> entschluessele(t,'INDW') 'MARTERPFAHLHEINERSPAEHTENACHUNTENABERVONHIERKONNTEERNICHTSERKENNENSICHERHABENWIRAUCHEINENMARTERPFAHL IHRWERDETIHNSCHONNOCHSEHENABEREIGENTLICHHEISSTDERGARNICHTMARTERPFAHLSONDERNTOTEMUN ......
Will man selbst Texte in obiger Art Vigenère-verschlüsseln, so wäre eine Funktion convert ganz praktisch, die Satzzeichen und Leerzeichen entfernt, die deutsche Umlaute umschreibt und die alle Buchstaben in Großbuchstaben umwandelt.
def convert(t):
"""
aus dem Text t werden Satzzeichen und Leerzeichen entfernt,
die deutsche Umlaute umschrieben und alle Buchstaben in
Großbuchstaben umgewandelt
"""
t = t.replace('ä','ae')
t = t.replace('ö','oe')
t = t.replace('ü','ue')
t = t.replace('Ä','AE')
t = t.replace('Ö','OE')
t = t.replace('Ü','UE')
t = t.replace('ß','ss')
t = t.replace(' ','')
t = t.replace('\n','')
t = t.replace('\r','')
t = t.replace(',','')
t = t.replace('.','')
t = t.replace('!','')
t = t.replace('?','')
t = t.replace(':','')
t = t.upper()
return t
Aufgabe 3
Entschlüssele nach obiger Anleitung folgenden Text:
KUSDVARKENTBCTQXBAHLQAAZNEFFONFVREATESFXSNRKCEYUCTIXBSPAELQXDEANXMHXXDVZUEVMENZNONQBQKRBDIFMNAFNXVRKWORZONFBMHFXSNRLFEELDAAWOSBAXEYXSTHGQEVGOSNGNEEXXZHUODVXXEALOLOLDVRKCCUNVDRMSSGWSEFXENZNONQBQKRBDWRGXDVXERFTMHRWORFXVBRGXIPADAZFKNTXVDRLFEELDAAWOSFHXDRKXDRKONGLMHYBOSFNXGHGNDRLWUGXCLVXQTFBMHFXSNRKYHAXVEVMENTXSNRLKNQXBEASEBRWSEAXXSNIORRTEDRAKBRFETQBMHQXSNRLOITXXEAOORFMKNQXCZHUODVXXEABCTNECOQXBWNAVSCKECUWORNNPKYTORHGQ
Aufgabe 4
Entschlüssele folgenden Text:
NWLWBATWIGSBYEMGMRSNGMSUKXMUIGIPVFEDWIOYPPZDWTVTAOTQEALTKIEMKICLXNNRRYGWDTATAVATCLWAKUZFMADUVTHUQEDBIGFULWWLLWPVTHHGQEGTATVOGQIPAGSBRKXIPVTKPKBLXPLZNZHWLTALMJTTAWEGMWMIEWGQMEKRZFSLIPVPTHARNWRWETBCCVSEXOYTENEVSMDNJONIPRFMTZWIOTUZLXHGFUPXTCSXTIIOVZAYAITLCIDTITAGCWETATJRRKTTFFMWQJCTCVFNIDQETLTFRCMAGKOPPZUSTCIIRHLDRLETGNIMWBYRXTERTXGNRLEHBYEOXBRLHCMZSMWMDIWSTVOGTAKAGSWETATNCAMGWTKTIBYEMDXFFMWMWAEAIEDNHQEGTRWDPTHACOHZLLEGDZKHRDCNIEAAVETHBLNMTLKRXTOIOPXVXOGPVRRKDECEWVMSEAXVUTAPBKRXTQJTATMETKPVTEMDBYEVPDVDBVCGTATNCOHGIEDRDCNIEANZNWBGFLWHMRCATAKFBATVDPXBYGHALJIEKMIAGSJRGLDNSETJBZFNAARPIWQIELPVUEFTZRLWHBYEKTIIETAAFSHBMTOLITPSIXKVSTCLRSMGIEGXVZVEGHBRTNTWWAGJVBNHLVXOWIPVTKTIJUKTQJYHJZJAGSQNILWGFUFDZVLNRSKHTCQKBKDCXHMBMDYEXNVHTHJVEGRCISXSAZNVTQWONCLZTTATZNMWIKCETIIIGVWEBHLMEILAIEDTBWEGLIBYEUDVVSTCLJKNATJOYIPIEXJVWOKICEAMTANHHWIUDBTLSEYDZVTATGTONALIEMJZEHHBMNIMWBYEBGNFRMJVVEUTVVESTZ
Aufgabe 5
Berechne mit Hilfe eines Programms für obigen Geheimtext der Länge n den Koinzidenzindex
.
Der Koinzidenzindex beträgt für einen
monoalphabetisch verschlüsselten deutschen Text etwa 0,0762. Überprüfe das an einem geeigneten Text.
Wenn der Index deutlich kleiner ist, so ist der Text nicht monoalphabetisch verschlüsselt.
Verwende den Koinzidenzindex, um mit Hilfe des Friedmann-Tests
die Schlüsselwortlänge h zu bestimmen.
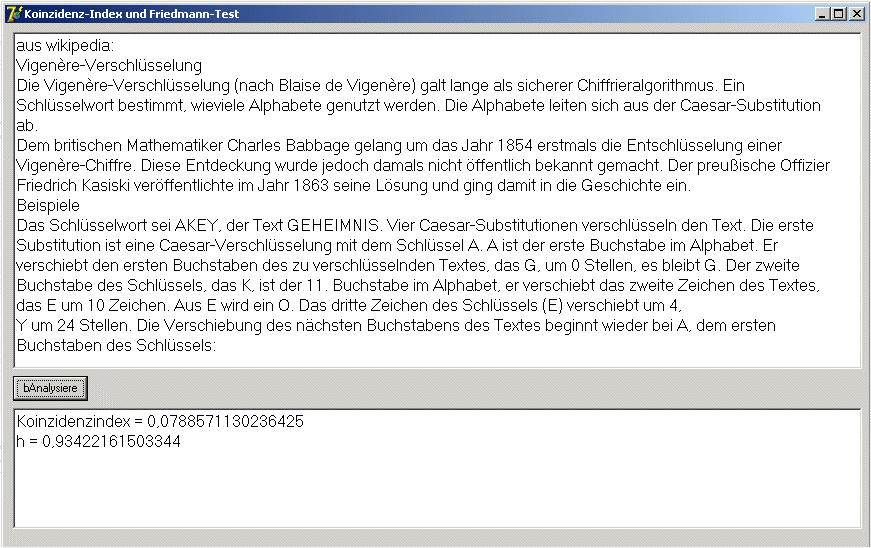koinzidenz.zip
Die Enigma
Die Enigma arbeitet ebenfalls nach dem Prinzip der
polyalphabetischen Verschlüsselung.